用Mathematica处理高等数学——幂级数问题初探

1、        Series[f[x],{x,0,n}]是把函数f(x)展开为x=0处的幂级数的近似形式。

Series[1/(1 + x + x^2), {x, 0, 6}]

        这是求1/(1 + x + x^2)的级数的前六项。

2、        二项式展开（只是展开一部分）：

Series[(a + b)^n, {b, 0, 3}]

        这里展开了四项。

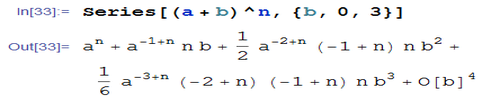
3、        对于未定义的函数，将用导函数的形式给出其幂级数：

Series[1 + g[t], {t, 0, 3}]

        如果要消去后面的剩余项，可以用Normal命令：

Normal[%]

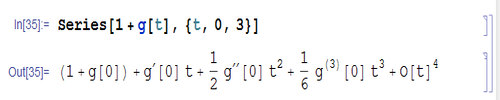
4、        Series展开的级数，有可能含有别的函数形式：

Series[x^x, {x, 0, 4}]

        这里就含有对数函数的形式。

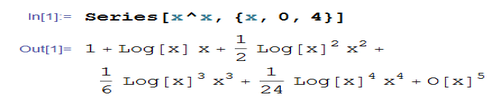
5、        如果难以求出函数的反函数，用InverseSeries命令可以直接求其反函数的级数。如求f(x)反函数的幂级数：

InverseSeries[Series[f[y], {y, 0, 3}], x]

1、        求级数1+1/1!+1/2!+……的和函数：

Sum[1/n!, {n, 0, Infinity}]

        其中，Infinity是无限大的意思。

2、        调和级数不收敛！

Sum[1/n, {n, 1, Infinity}]

        但是，Mathematica能精确地求出它的部分和：

Sum[1/n, {n, 1, 99}]

3、        类似于调和级数的p-级数（p>1）都是收敛的：

Sum[1/n^2, {n, 1, Infinity}]

        多列举几个看看：

Table[Sum[1/n^p, {n, 1, Infinity}], {p, 2, 10, 1}]

        当p是奇数的时候，无法给p-级数得出明确的结果，但是这些级数都是收敛的！所以用Zeta函数来表示。

4、        不规则级数求和，也有可能得到和函数。例如：

Sum[1/(a^2 + x^2), {x, 1, Infinity}]

Sum[1/(a^2 + x^2), {a, 1, Infinity}]

5、        连续自然数的幂和公式的Mathematica代码（幂指数分别是1， 2， 3， 4， 5）：

Table[Sum[a^b, {a, 1, x}], {b, 5}]

1、        这里用到的是SeriesCoefficient，可翻译为——级数系数，它有可能给出函数展开为幂级数的系数的通项公式。例如，求正割函数的幂级数系数的通项公式：

SeriesCoefficient[1/Cos[x], {x, 0, n}]

2、        有些幂级数的系数要用特殊函数来表示，如函数1/(x^2 - 3 x + 1)的幂级数系数要用到切比雪夫函数：

SeriesCoefficient[1/(1 - 3 x + x^2), {x, 0, n}]

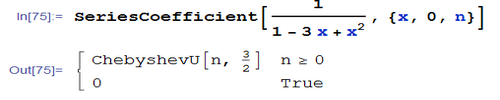
3、        Fibonacci 数的生成函数是1/(1 - t - t^2)，这样就可以求出Fibonacci 数的通项公式：

SeriesCoefficient[1/(1 - t - t^2), {t, 0, n}]

Fibonacci[n]

        关键是要知道生成函数是什么！

4、        绘制一个关于各种函数幂级数的表格：

hanshuliebiao = {Exp[x], Sin[x], Cos[x], 1/(1 + x), Log[1 + x],    ArcTan[x]};

Grid[Join[{{f[x], Text["级数系数"]}}, 

   Transpose[{hanshuliebiao, 

     Map[SeriesCoefficient[#, {x, 0, n}] &, flist]}]], 

  Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> 

      Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, 

  BaseStyle -> {FontFamily -> Times, FontSize -> 12}, Dividers -> All,

   FrameStyle -> Hue[.6, .4, .8], 

  Spacings -> {2, 1}] // TraditionalForm