椭圆的第二定义
第二定义:
椭圆平面内到定点 F(c,0)的距离和到定直线 L:

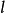

(即离心率 e,0<e<1)的点的轨迹是椭圆。其中定点
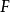
(该定直线的方程是



扩展资料:
其他定义:
根据椭圆的一条重要性质:椭圆上的点与椭圆长轴(事实上只要是直径都可以)两端点连线的斜率之积是定值,定值为

在坐标轴内,动点(


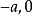
注意:考虑到斜率不存在时不满足乘积为常数,所以
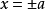
无法取到,即该定义仅为去掉四个点的椭圆。
椭圆也可看做圆按一定方向作压缩或拉伸一定比例所得图形。
参考资料:百度百科-----椭圆
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:118
阅读量:173
阅读量:68
阅读量:29
阅读量:114