圆的面积教学设计

1、（一）创设情境，激发兴趣。1.出示情境图，提出问题：拴在书上的马儿的最大活动范围在哪里？那么这个最大的活动范围是什么呢？如果拴马儿的绳长是2米，马儿的最大活动范围到底是多大呢？（其实就是求半径是2米的圆的面积）2.明确圆的面积的概念:圆所占平面的大小叫做圆的面积。

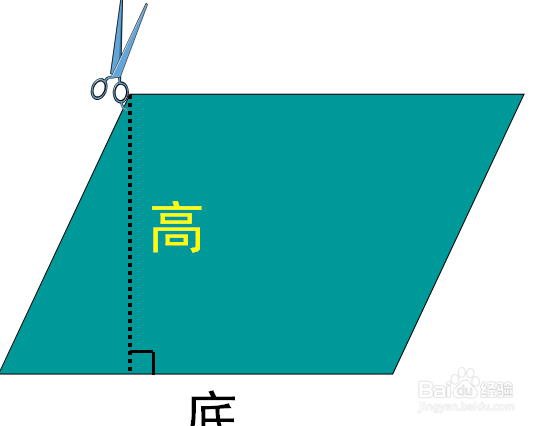
2、（二）探究方法。1.回想一下，我们是怎样的到平行四边形、三角形和梯形的面积公式的？（以平行四边形为例）。2.我们将圆转化成什么样的图形来推导它的面积计算公式呢？【通过回顾原有的知识体系，激发学生知识的迁移，为后面自主探究圆的面积计算公式奠定了基础。】

3、（三）实践操作。1.动手试一试，剪一剪并拼一拼，想想怎样剪拼更好，看看能拼成什么图形？并且等分的份数越多会怎样？【在刚才这个动手操作的过程中，放手让学生通过比较得出沿半径剪拼的方法是较为科学的，在教学中注重对学生进行思维方法的指导，给学生提供了自行探究，创造性寻找解决问题的方法和途径，再通过电脑课件的演示，生动形象地展示了化曲为直的剪拼过程。使学生进一步明确拼成的平行四边形与圆之间的对应关系，有效地认识和理解圆转化成平行四边形的演变过程。】2.通过观察比较，看看当圆转化成近似的平行四边形后，它们之间有什么关系？（1）圆的形状发生了变化，但面积的大小没变。（2）平行四边形的底就相当于圆周长的一半，平行四边形的高就相当于圆的半径，因为平行四边形的面积=底×高，那么圆的面积就是圆周长的一半×半径，用字母表示为s=∏r×r=∏r2,,所以圆的面积公式是s=∏r2。【在学生的动手操作，推导中建立数学模型。】

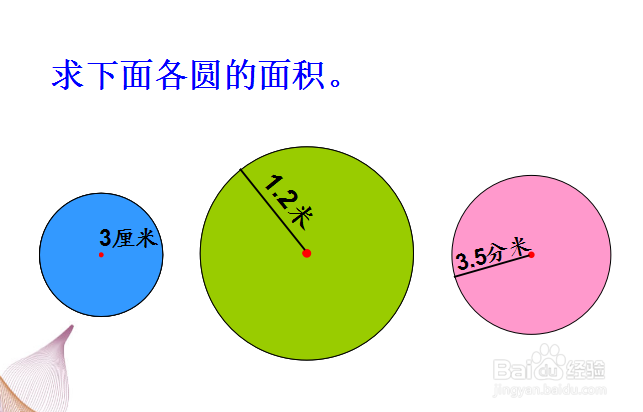
4、（四）巩固练习。1.用所学的知识解决马儿的困惑。s=∏r2=3.14×2×2=12.56平方米。【回应了开头，使课堂形成了一个完整的体系，也体现了知识的学有所用。】2.求下面圆的面积。（1）r=3厘米（2）r=1.2米（3）r=3.5分米3.已知圆的直径求圆的面积。出示题目：一个雷达屏幕的直径是40厘米，它的面积是多少平方厘米？（先求出半径）4.已知圆的周长求圆的面积。出示题目：街心花园中圆形花坛的周长是18.84米。花坛的面积是多少平方米？（先求出半径）5.总结：知道圆的半径、直径或是周长都可以求出圆的面积。6.易错点练习（判断正误）（1）直径是2厘米的圆，它的周长和面积相等。()（2）两个圆的周长相等，面积也一定相等。（）（3）圆的半径越大，圆所占的面积也越大。（）（4）圆的半径扩大3倍，它的面积扩大6倍。（）（5）半圆的面积是它的整个圆面积的一半。

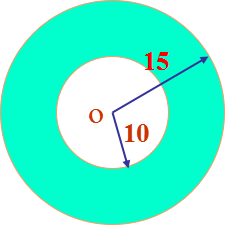
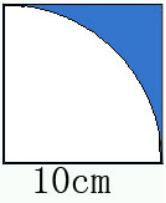
5、（五）拓展练习：求阴影部分的面积。【练习由易到难，由浅到深，练习有层次有梯度，课堂容量大，有基础练习也有易错点的指导，还有拓展练习，学生的思维得到了提升。】（六）作业。求圆环的面积（链接下节课内容）。