椭圆的作图问题:椭圆中心、对称轴、焦点、切线
1、 第一个问题:给定椭圆,要求找出椭圆的中心。这个所谓的中心,就是椭圆的两个焦点的中点。
先介绍一个结论:椭圆的平行弦的中点之轨迹是一条直线,如图。如此一来,就可以作出椭圆上有固定方向的切线。
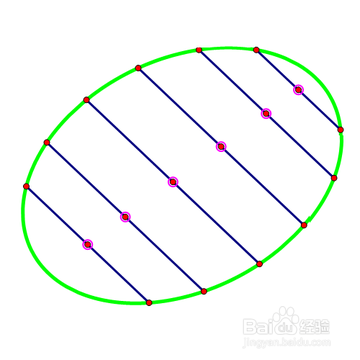
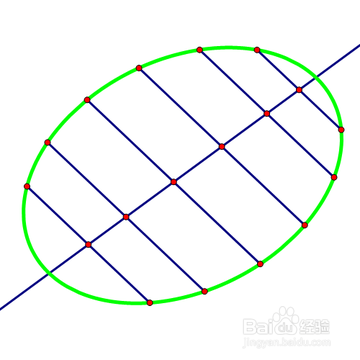

2、 给定椭圆,这个时候给出的椭圆光溜溜的,看不出任何线索指向它的中心,这就需要用到上面那个结论。

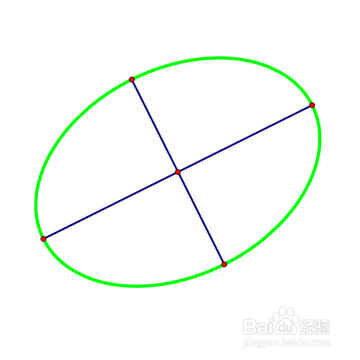
3、 先在椭圆上构造两对平行弦。
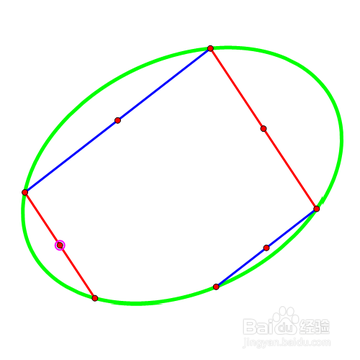
4、 分别连结每一对平行弦的中点为直线,那么两条直线的交点就是椭圆的中心,记为点O。
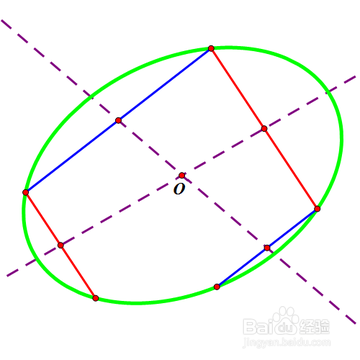

1、 第二个问题:作椭圆的对称轴和焦点。
椭圆有两条对称轴,分别是长轴和短轴。上面已经找到了椭圆的中心,趁此机会,把椭圆的对称轴和焦点也一起找出来。
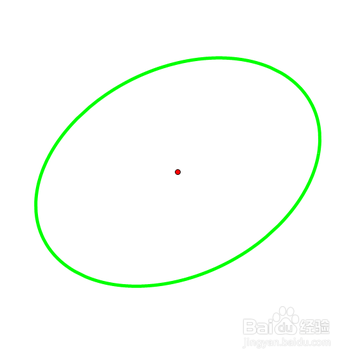
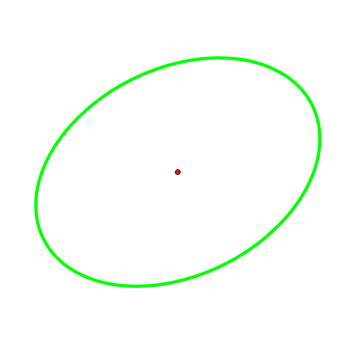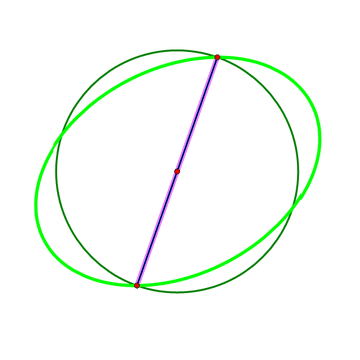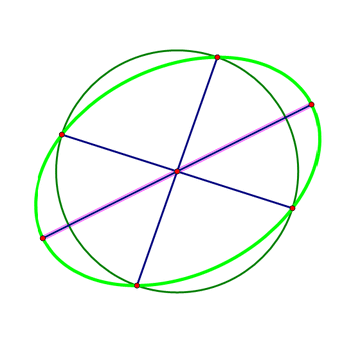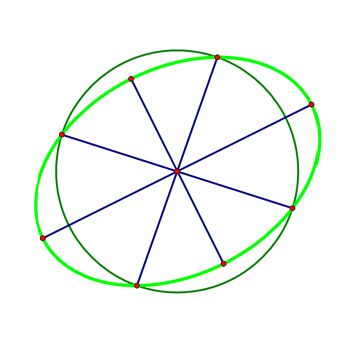
2、 以椭圆的中心O为圆心作一个大小适度的圆,与椭圆交于四个点。这四个点围成一个矩形,对角线交于O点。
那么,对角线夹角的平分线,就是椭圆的对称轴所在的直线。于是,椭圆的长轴和短轴也就做出来了。
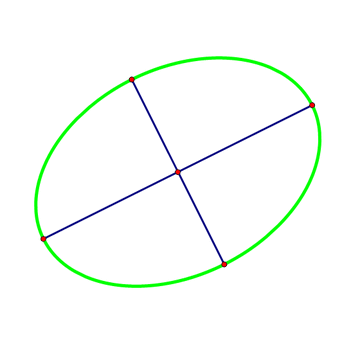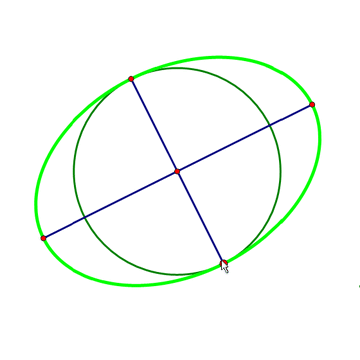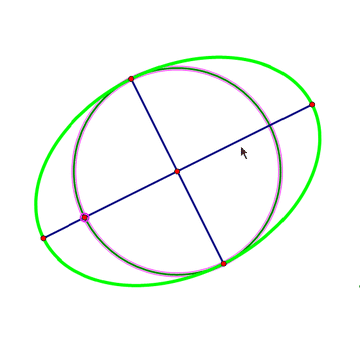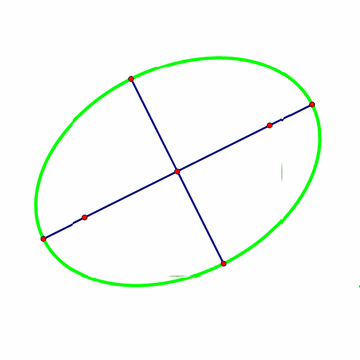
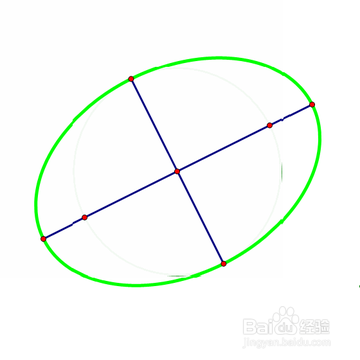
3、注意,下图的方法是错的。
正确方法是:以短轴端点为圆心、半长轴为半径作圆,与常州的两个交点,就是椭圆的焦点。
1、 第三个问题:作点X关于椭圆的切线。
当点X位于椭圆上的时候,可以利用椭圆的光反射特性来作图。椭圆的光反射特性指的是:假设椭圆内表面是光滑的镜面,那么,从其中一个焦点发出的光线,经过椭圆的反射,将会会聚于另一个焦点。
所以,点X到两个焦点的连线的夹角的外角平分线就是X关于椭圆的切线。



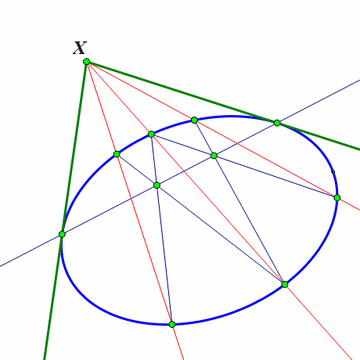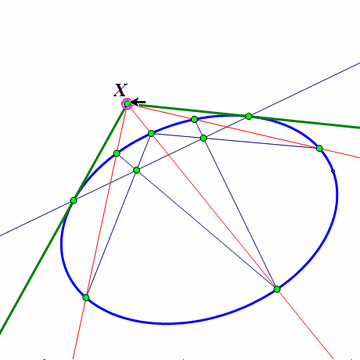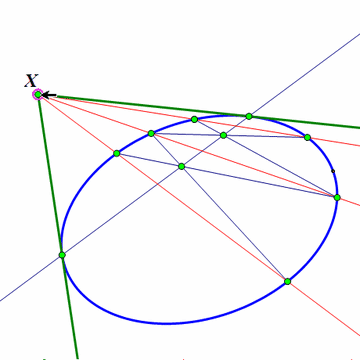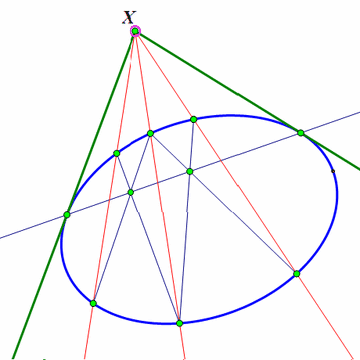
2、 当X位于椭圆外面的时候,可以利用射影几何学里面的极点极线原理来做图。这个东西的详细内容,请移驾——《射影几何学的正确入门方法》。
作图方法是:作点X关于椭圆的极线;那么,这条极线与椭圆的两个交点,就是X到椭圆的切线的切点。