利用Python处理数据(搜索函数)
1、明确概念:
编辑距离(Edit Distance),又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。一般来说,编辑距离越小,两个串的相似度越大。
我们根据编辑距离来对数据进行处理,匹配。
限制编辑距离的阈值来控制字符串的相似度。

2、编辑距离的算法:
以下是对编辑距离的介绍:
使用动态编程思想,构造一个矩阵,初始化是第一列和第一行的数值等于其行索引和列索引,其余数值均按照下述方法填充。

3、原始数据:将原始数据作为索引从另一份数据中即数据库中调取,按照原始数据中的某一列作为索引,由于数据来源不同,可能存在拼写错误、缩写等不同,切不知道差异程度。故采用本函数处理。

4、数据库:调取数据的存储文件。
为原始数据提供数据的源。

5、源代码:
import numpy as np
import pandas as pd
from pandas import DataFrame
T=5
#return_minimun_value
def minimun(one ,two ,three):
min=((one if one<two else two) if (one if one<two else two)<three else three)
return min
#calculate_similarity
def similarity(str_1,str_2):
d=np.zeros((len(str_1)+1,len(str_2)+1))
for i in range(len(str_1)+1):
d[i][0]=i
for j in range(len(str_2)+1):
d[0][j]=j
for i in range(1,len(str_1)+1):
for j in range(1,len(str_2)+1):
score=1
if str_1[i-1]==str_2[j-1]:
score=0
d[i][j]=minimun(d[i-1][j]+1,d[i][j-1]+1,d[i-1][j-1]+score) if minimun(d[i-1][j]+1,d[i][j-1]+1,d[i-1][j-1]+score)<T else 100
return d[len(str_1)][len(str_2)]
#indentify_how_similar
def identify(s1,s2):
s1=s1.strip()
s2=s2.strip()
s1=s1.split(' ')
s2=s2.split(' ')
t=len(s1) if len(s1)<len(s2) else len(s2)
score=0
for i in range(t):
if s1[i]!=s2[i]:
score=100
break
score=score+similarity(s1[i],s2[i])
return score
path1='C:\\Users\\jyjh\\Desktop\\chromosome_data.csv'
path2='C:\\Users\\jyjh\\Desktop\\xishaislands.csv'
cd=pd.read_csv(path1,index_col=0)
xs=pd.read_csv(path2)
cd=DataFrame(cd)
xs=DataFrame(xs)
cdlt=[]
xslt=[]
for i in cd['Latin_name']:
cdlt.append(i)
for i in xs['latin_name']:
xslt.append(i)
dic={}
for j in range(len(xs.index)):
locc=0
loc=0
sms=[]
for i in cdlt:
sms.append(identify(i,xs['latin_name'].ix[j]))
min=sms[0]
for i in sms:
if i<min:
min=i
locc=loc
loc=loc+1
dic.setdefault(xs['latin_name'].ix[j],locc)
col=['Gametophytic','Sporophytic','Paresd_n']
data=DataFrame(index=dic.keys(),columns=col)
all=[]
for i in dic.values():
if i!=0:
all.append(cd['Gametophytic'].ix[i])
else:
all.append(' ')
for i in arange(len(dic.keys())):
data['Gametophytic'].ix[i]=all[i]
all=[]
for i in dic.values():
if i!=0:
all.append(cd['Sporophytic'].ix[i])
else:
all.append(' ')
for i in arange(len(dic.keys())):
data['Sporophytic'].ix[i]=all[i]
all=[]
for i in dic.values():
if i!=0:
all.append(cd['Paresd_n'].ix[i])
else:
all.append(' ')
for i in arange(len(dic.keys())):
data['Paresd_n'].ix[i]=all[i]
data.to_csv('data.csv')
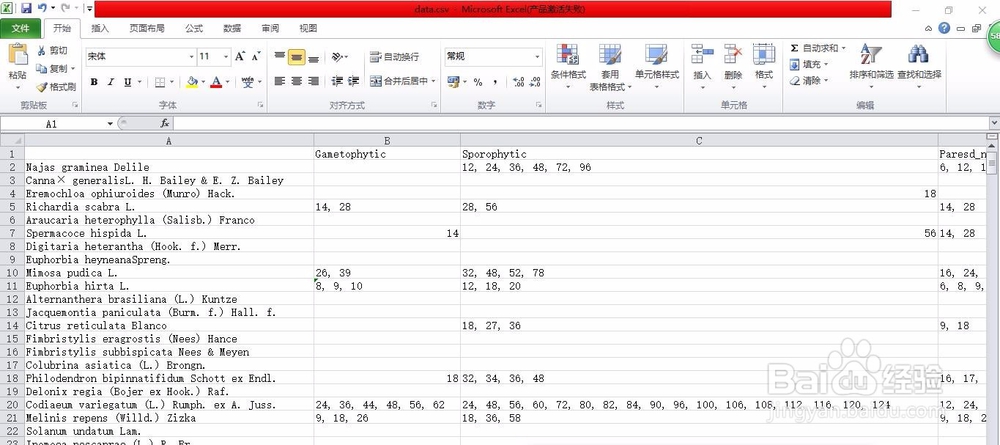
6、结果:
输出data.csv文件
查看结果,并对阈值做一定修改以优化函数。