【微分几何】怎么绘制两个圆环面的公共部分?
1、相交区域的表示方法,可以借助不等式组。
这就需要算出两个圆环面的隐函数方程。
先算r1的隐函数方程:
(x^2 + y^2 + z^2)^2 - (10 x^2 + 10 y^2 - 6 z^2) + 9=0
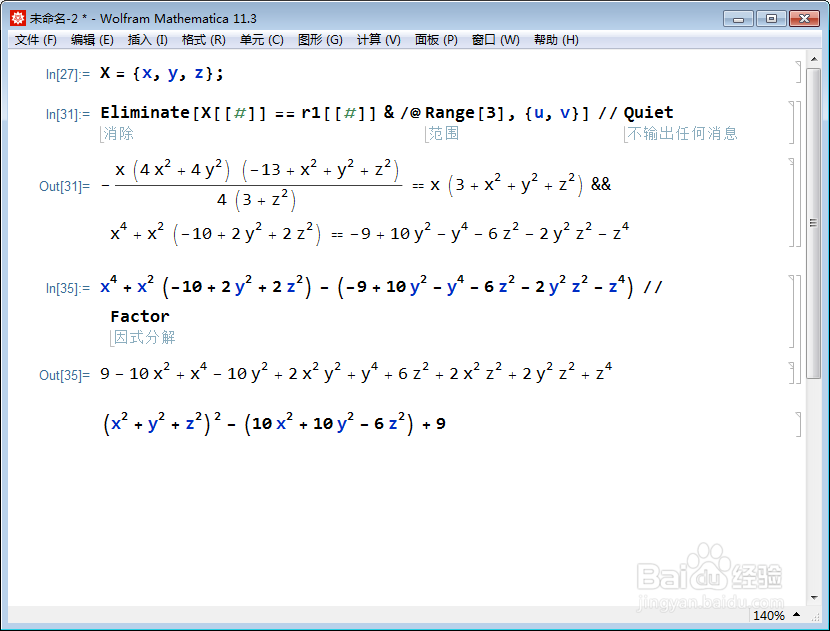
2、再算r2的隐函数方程:
(x^2 + y^2 + z^2)^2 - 16 x (x^2 + y^2 + z^2)
+ (86 x^2 + 38 y^2 + 22 z^2) - 176 x + 105=0

3、使用RegionPlot3D,就可以作出不等式组所代表的区域图像:
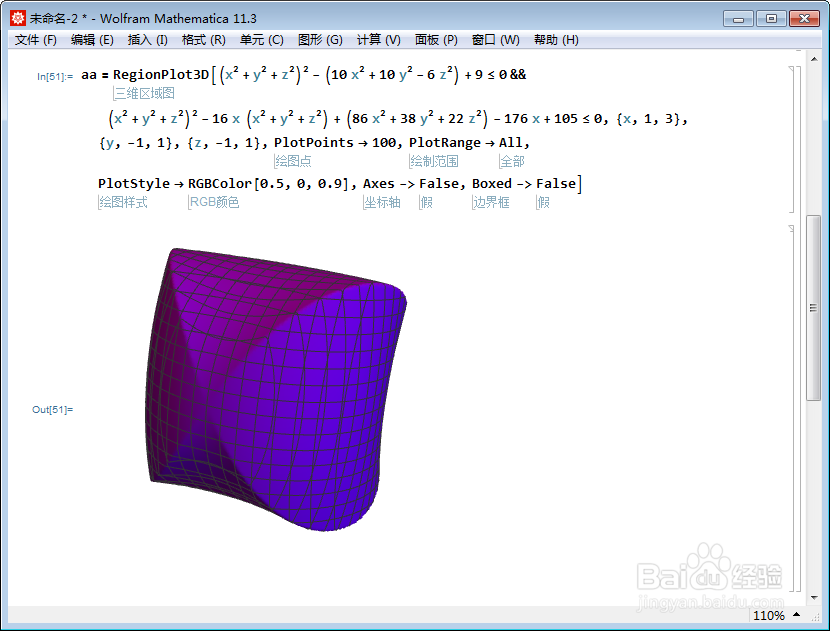
4、输出动态图:

5、在原图中,凸显公共区域:

6、如果r2变为{2 + (2 + Cos[u]) Cos[v], -Sin[u], (2 + Cos[u]) Sin[v]},就是一个与r1扣在一起的圆环。
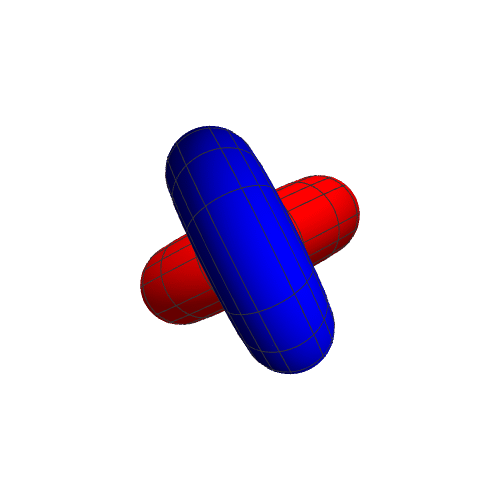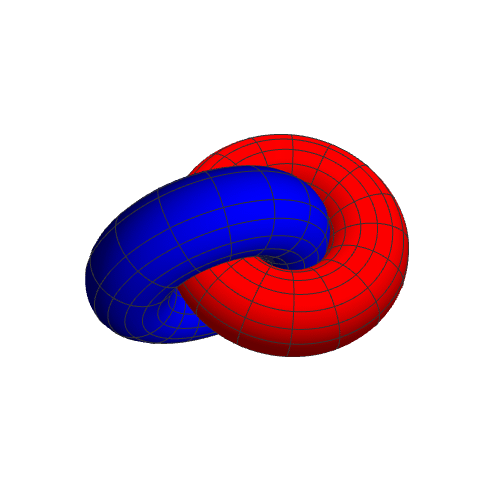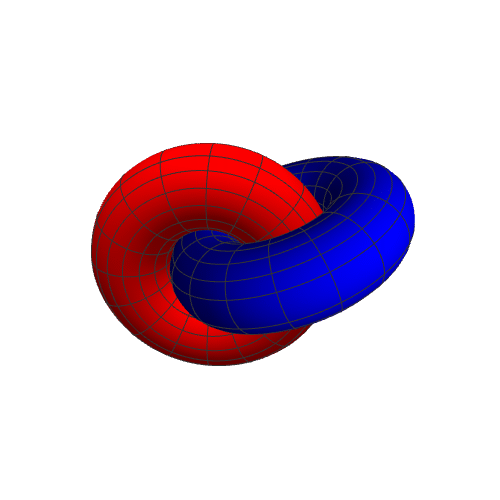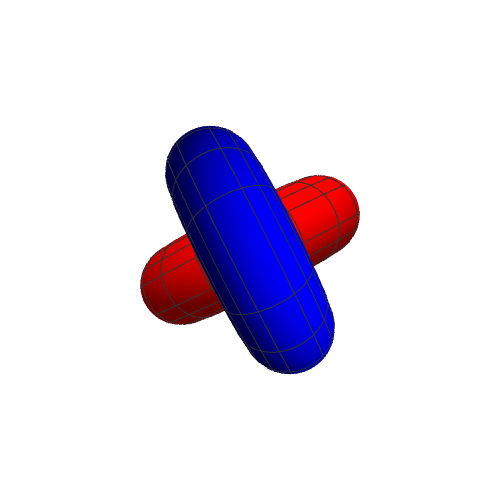
7、r2={(2 + Cos[u]) Cos[v], -Sin[u], (2 + Cos[u]) Sin[v]},表现如下:
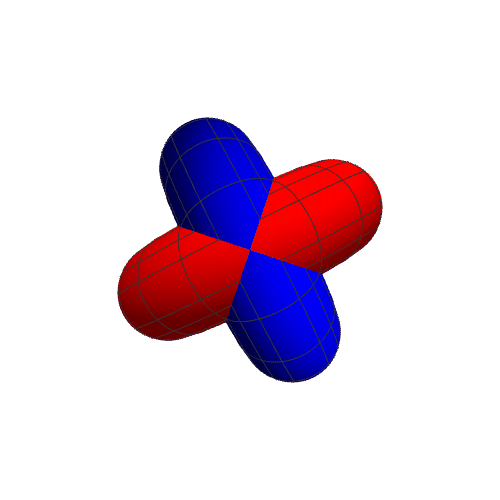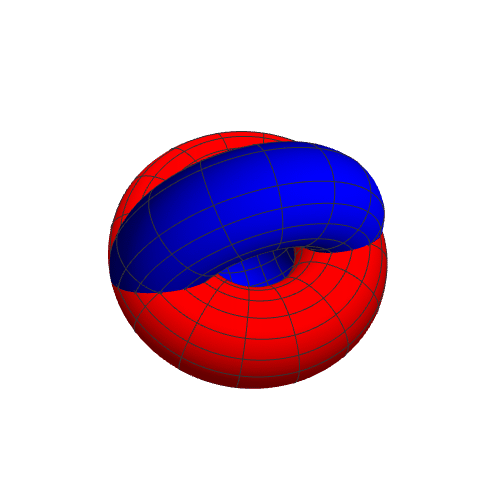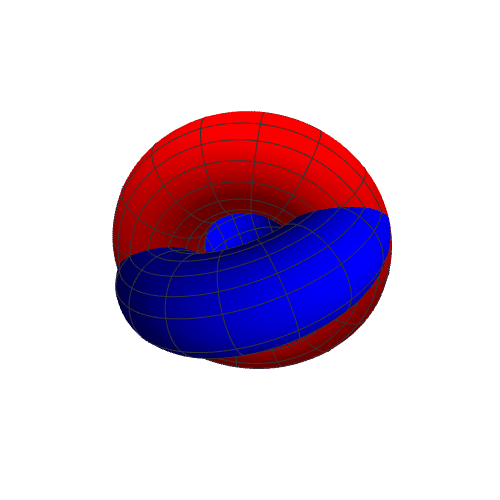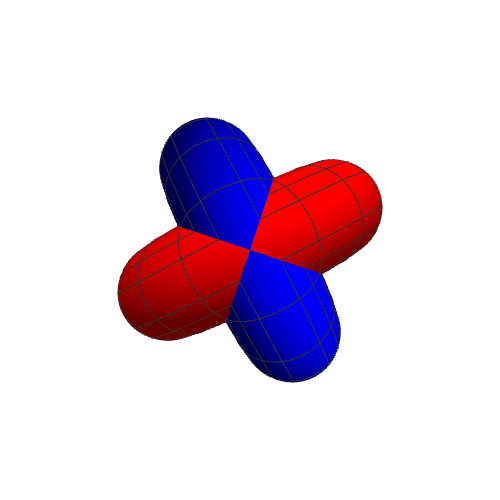
8、此时公共区域是两个分离的部分:

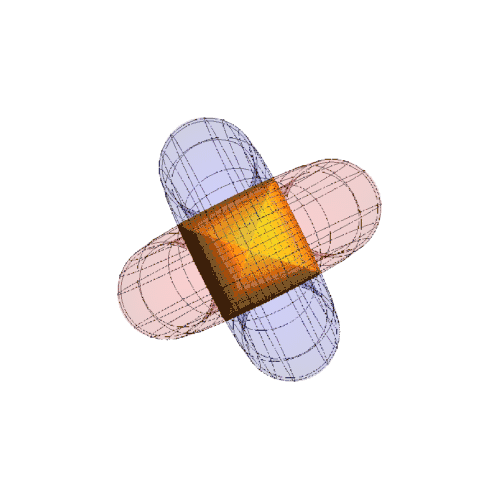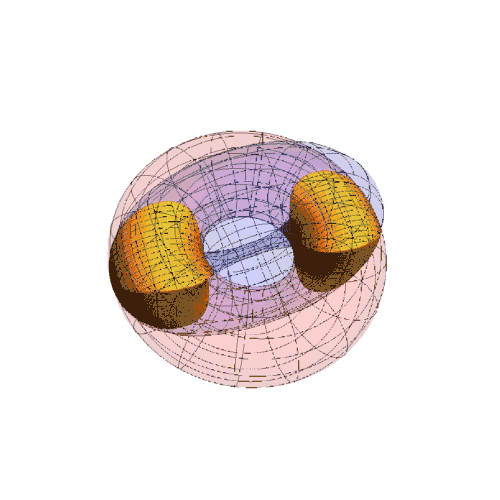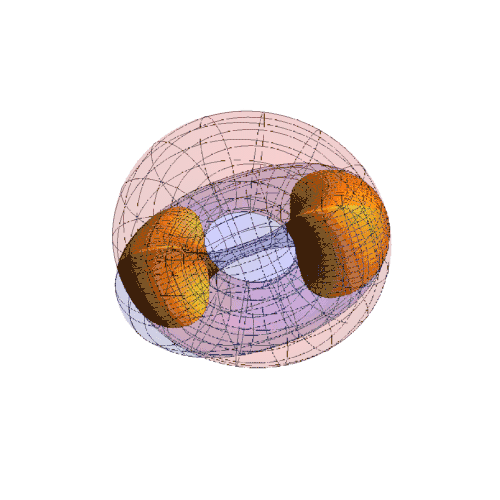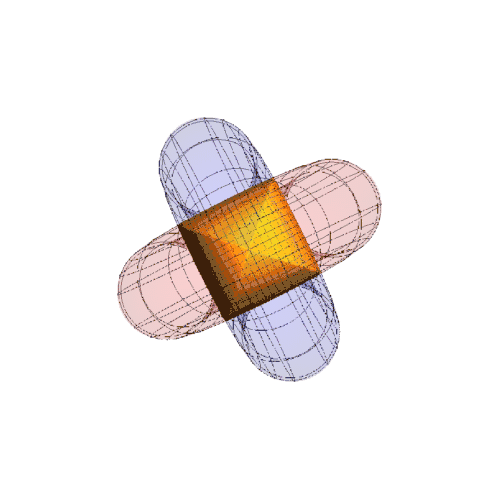
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:155
阅读量:171
阅读量:54
阅读量:76
阅读量:103