用Mathematica演示圆的各种摆线——内摆线
当一个圆在另一个圆上均匀的滚动,前者上面的某个点的轨迹,是一个非常精美的图形;这是天体运动的一种简化模型,假设所有的天体的运行轨道都是圆形。
即使是简化模型,当要处理若干天体的运动轨迹也是很复杂的。
比如,月球——地球——太阳——银河系中心,这是一个四级绕转系统,假设日地月的绕转轨道都是圆形,那么,以银河系中心为原点,月球的运动轨迹是个什么图形呢?是不是很复杂?
这里不考虑复杂的问题,只研究一个圆在另一个圆内部滚动的情形,工具是Mathematica。
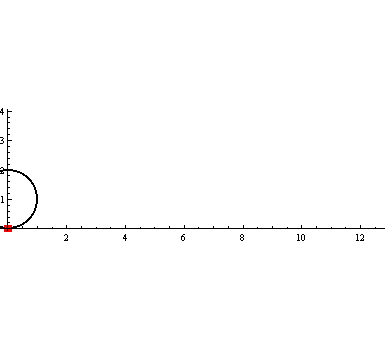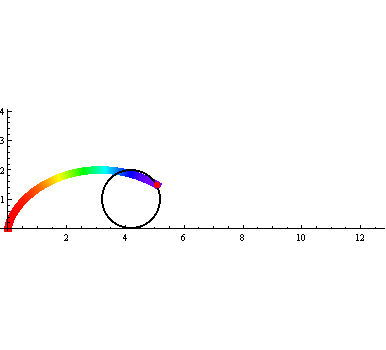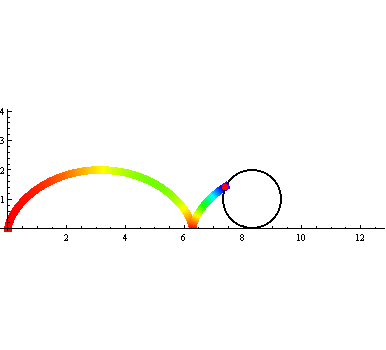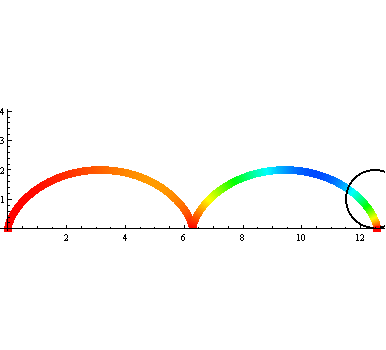
工具/原料
电脑
Mathematica
摆线
首先,我们把直线当成是半径很大的圆,大到无法想像的程度。这样,圆在直线上滚动,就相当于圆在另一个圆内滚动。我们把圆上的某个定点指定为“被追踪点”,当这个点在平面内移动的时候,会产生一条轨迹曲线。
圆在直线上滚动,“被追踪点”的轨迹称为“摆线”。它的参数方程是:{x=t - sint,y= 1 - cost}。

动画模拟:
把“被追踪点”定为蓝色、大小为0.1,它的轨迹为红色、粗细度0.02。
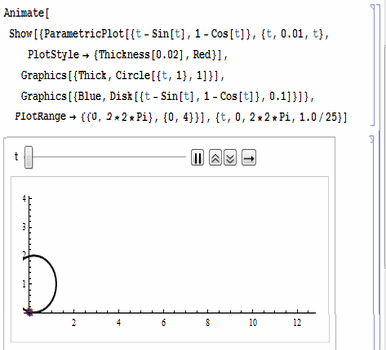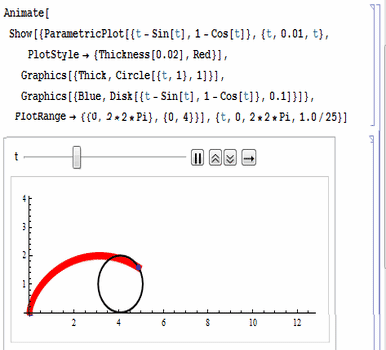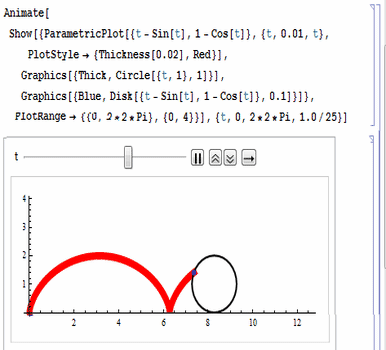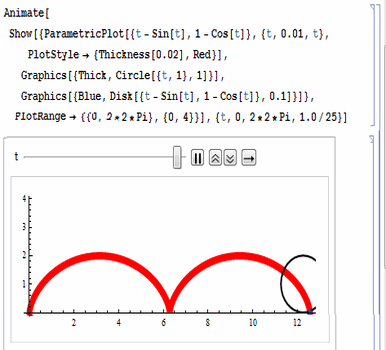
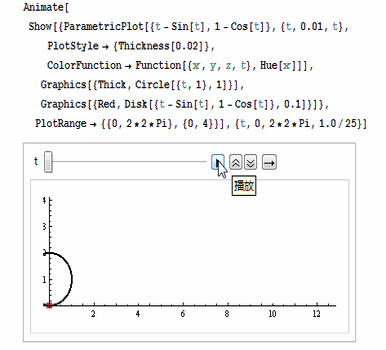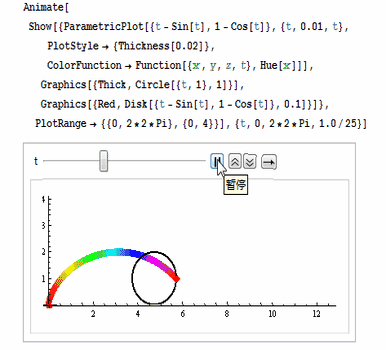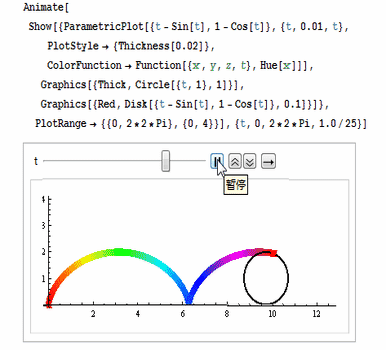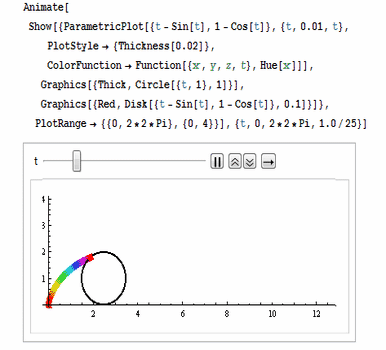
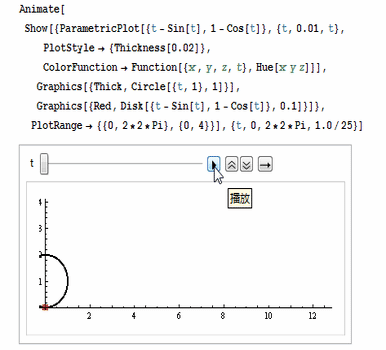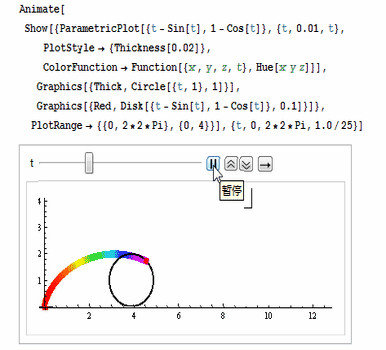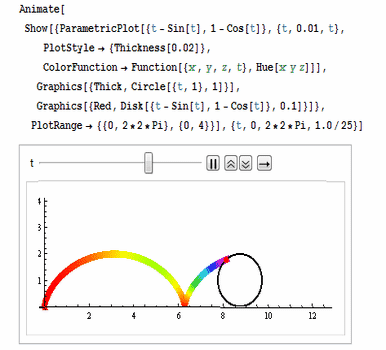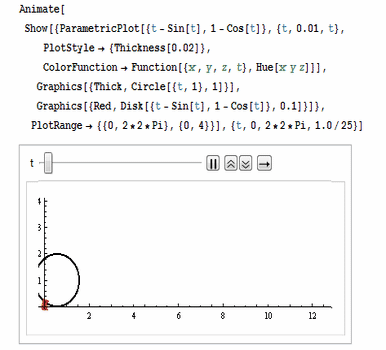
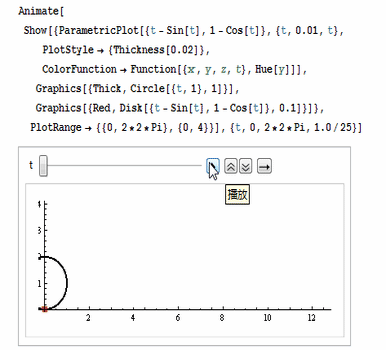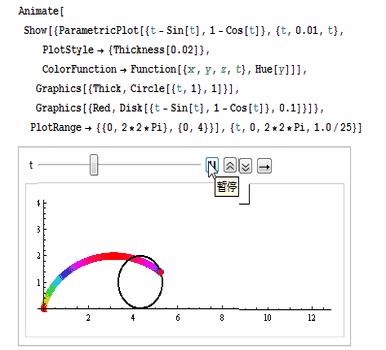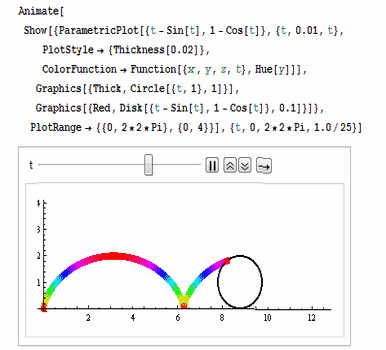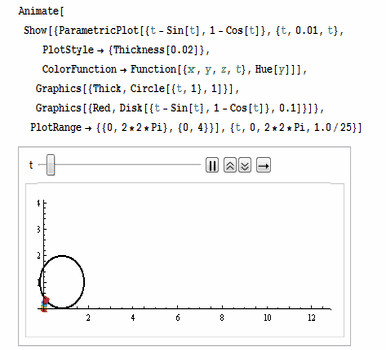
代码如图:
注意各项参数的设置,尤其是动画控制参数。(下面的图片被后期处理的时候压扁了,所以看着圆形是个椭圆形。)
还可以用ColorFunction把颜色设置为彩色,如图:
内摆线
圆A在另一个圆B的内部滚动,“被追踪点”在圆A上,其轨迹就是“内摆线”。
内摆线的参数方程是{x=(R-r)cos(t/R)+Rcos((R-r)t/(Rr)),y=(R-r)sin(t/R)-rsin((R-r)t/(Rr))};
小圆圆心在时间t的位置是((R - r) cos (t/R),(R - r) sin (t/R));
被追踪点在时间t的位置是((R - r) cos (t/R) + Rcos ((R - r)/Rr t),(R - r) sin (t/R) + Rsin ((R - r)/Rr t))。

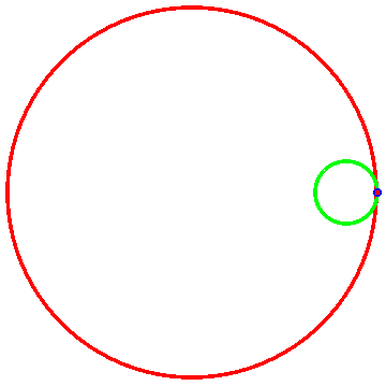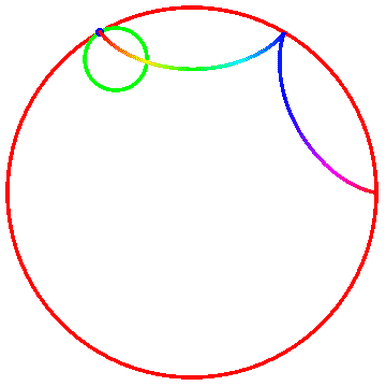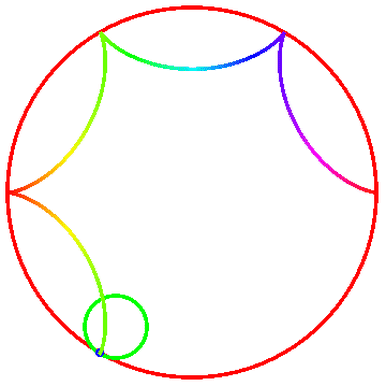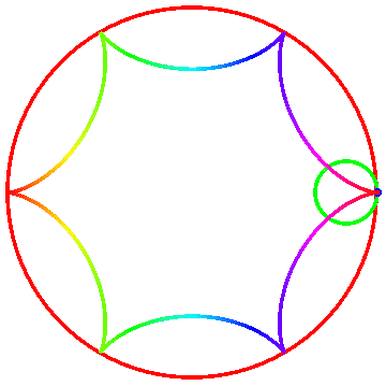
绘制圆A绕圆B的模拟滚动:
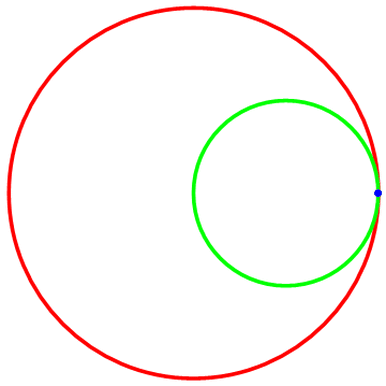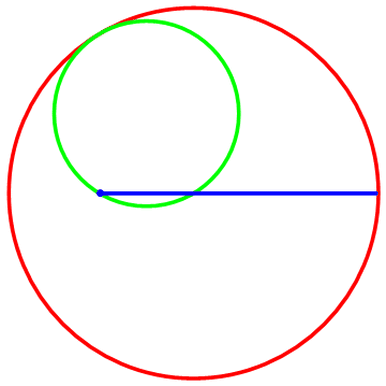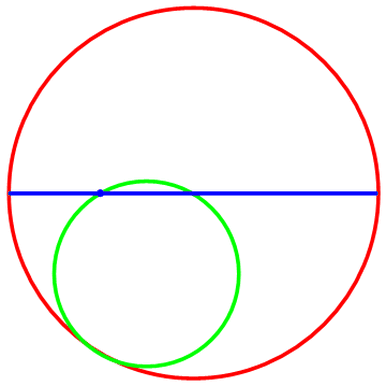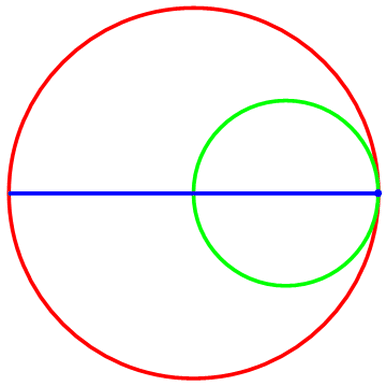
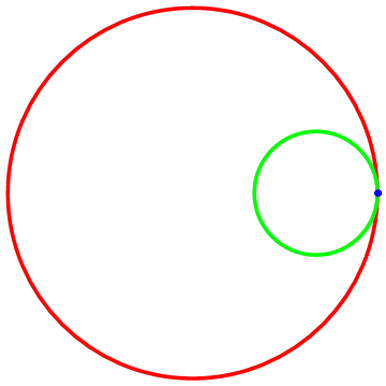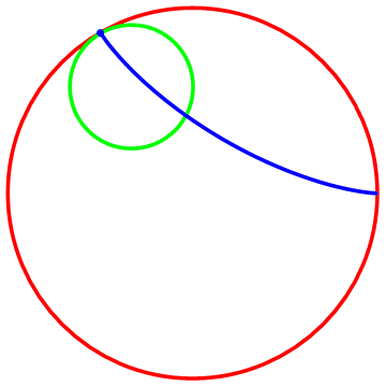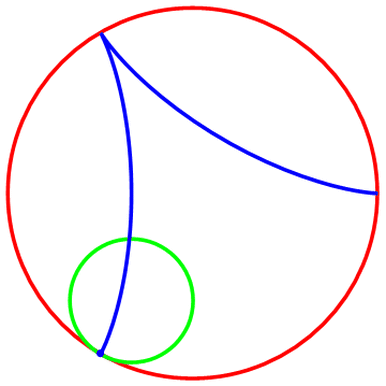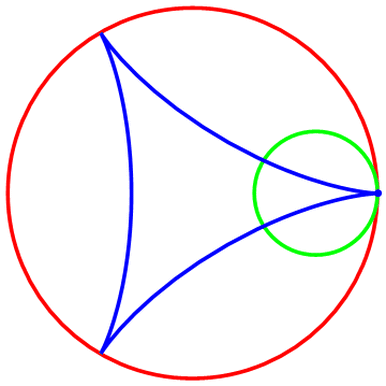
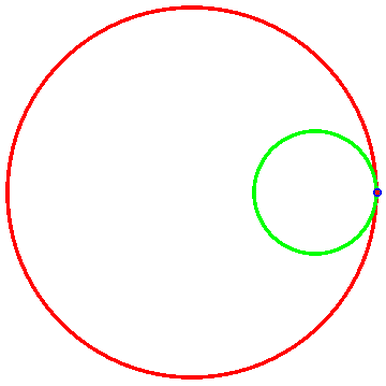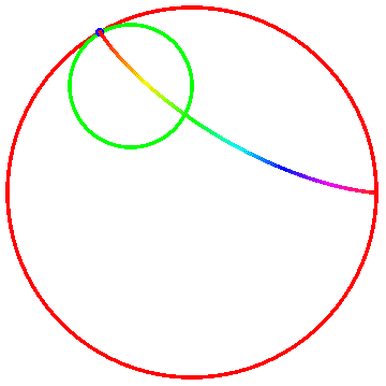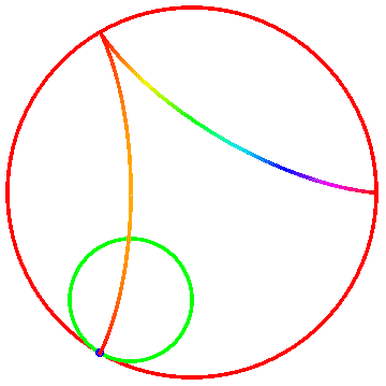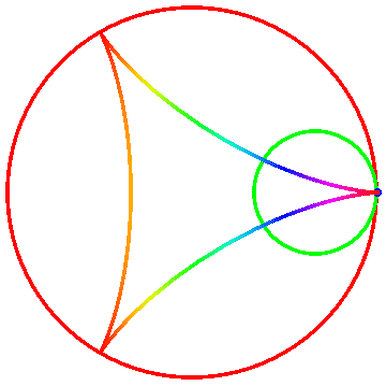
圆A是绿色的,圆B是红色,线的粗细度是0.01;“被追踪点”是蓝色,大小为0.2;暂时忽略“被追踪点”的轨迹和两圆圆心。
代码如图,代码里的R和r请手动调整;然后是导出的动态图及其代码。

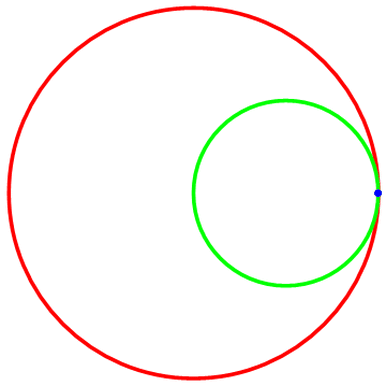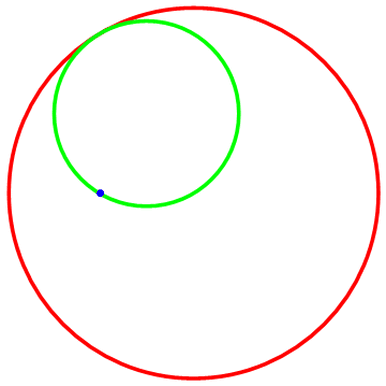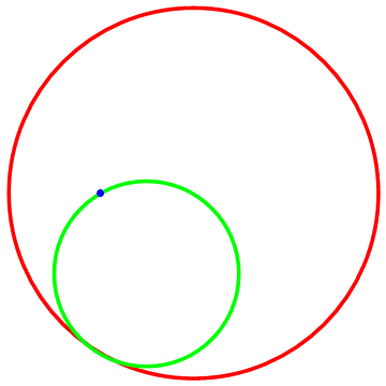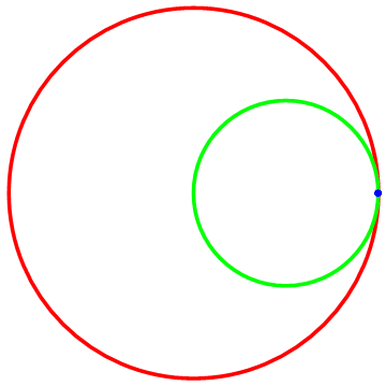

下面把“被追踪点”的轨迹——“内摆线”加上去,代码如图:
当R=2,r=1时,描绘出的“内摆线”是一条线段;
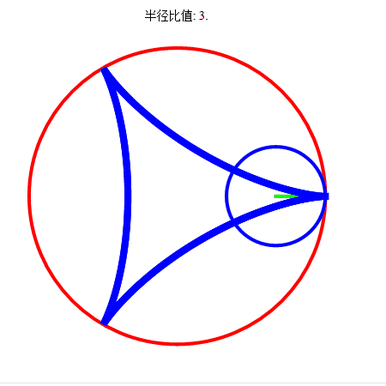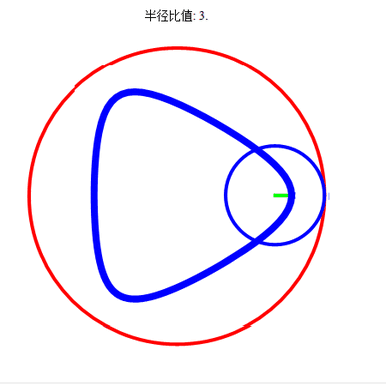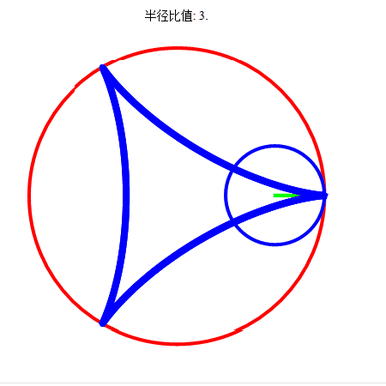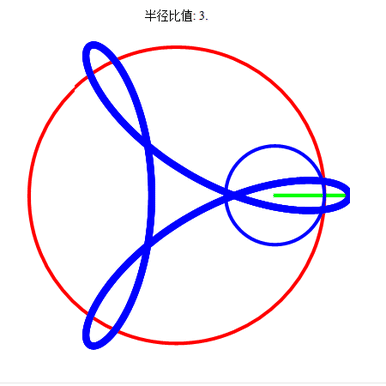
当R=3,r=1时,描绘出的“内摆线”是“三尖内摆线”;
其余的,就不再一一赘述,读者只需要调整R和r的值,然后分别运行即可。


把“内摆线”变成彩色,用到的函数命令仍旧是ColorFunction。
把R设为3,r=1,然后运行下面的代码:

内摆线的拓广
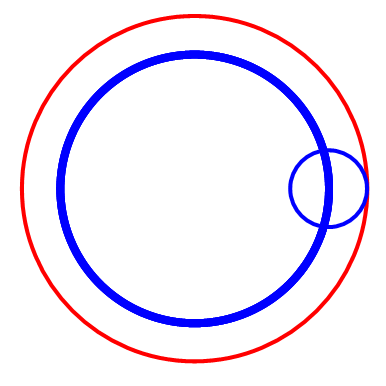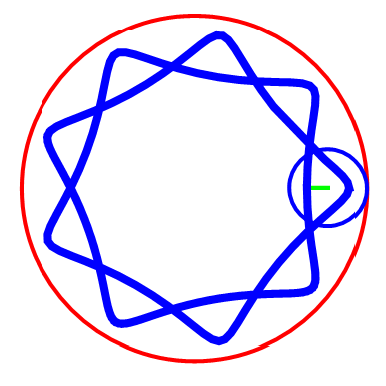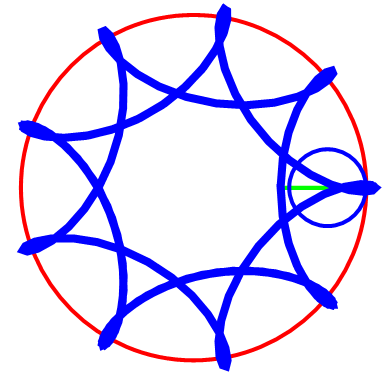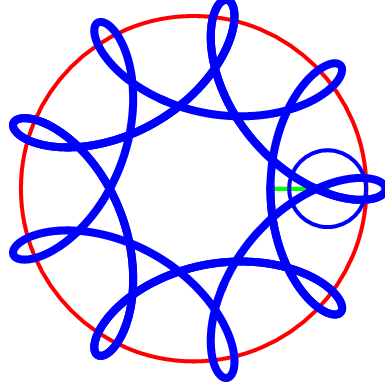
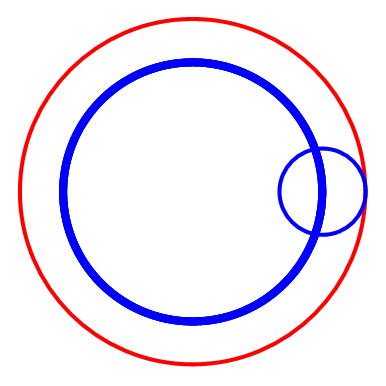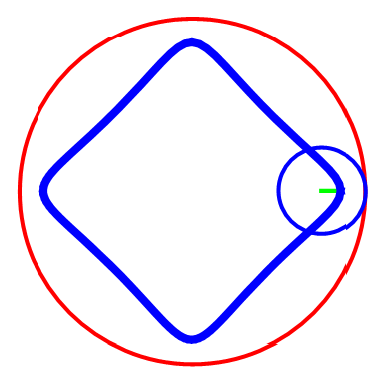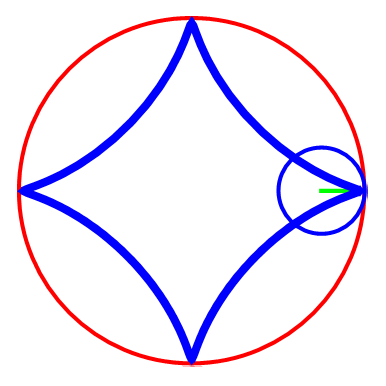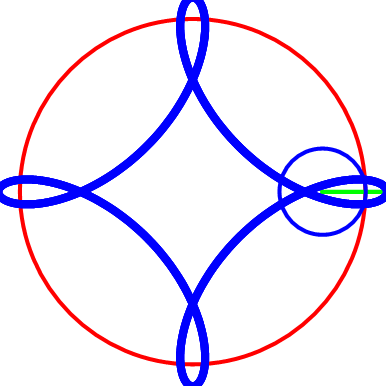
圆A在圆B上滚动,但是“被追踪点”不在圆A上,而是在圆A的内部或者外部。我们约定,“被追踪点”到圆A圆心的距离是d,那么,d>0 && d≠1。

一些预处理和自定义函数:
Clear[R, r, t, d](*虽然参数t没有专门定义过,但Mathematica在运行的时候,已经给t赋值了,所以必须清理*);
lctr[t_, r_] := (R - r) {Cos[t/R], Sin[t/R]}(*小圆圆心在时间t的位置*);
pt[t_, r_, d_] := lctr[t, r] +RotationMatrix[2 Pi - t/r].{d r Cos[t/R], d r Sin[t/R]}(*被追踪点在时间t的位置*);
先运行这些预处理和自定义,再运行图中的代码。代码先把R赋值为3,再通过改变r和d的值,画出不同的曲线。


截取几幅图看看。

注意事项
注意代码的先后顺序,以及图形线条的覆盖关系。
观察Graphics绘图时,对曲线颜色、粗细是如何设定的。
代码的主体部分都是截图,有助于大家练习打字速度,更好地理解代码的每一部分。
体会ColorFunction的用法,你可以尝试把Hue[x]换成Hue[y]、Hue[x y]或Hue[t],看看运行结果有什么不同,并思考为什么。
绘制不同零件的时候,我是分别用Graphics实现的。其实,也可以“提取公因式”,代码会更简短。
摆线的绘制,是使用ParametricPlot实现的。
有什么不明白的,可以私信联系我。如果这片经验对你有帮助,就把它推荐给你的朋友吧!