用Mathematica模拟双摆

1、双摆系统在任意时刻的受力分析图。

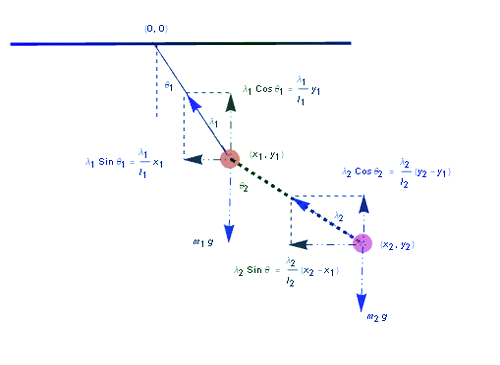
2、根据牛顿第二运动定律，可以总结出4个微分方程。

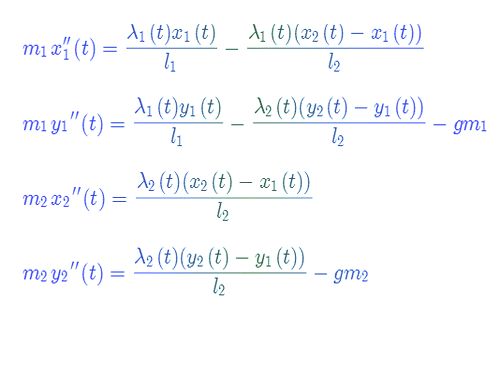
3、把上面的四个微分方程，视为一个微分方程组：

fcz = {Subscript[m, 1] x1''[t] == (\[Lambda]1[t]/Subscript[l, 1]) x1[t] - (\[Lambda]2[t]/Subscript[l, 2]) (x2[t] - x1[t]), 

   Subscript[m, 1] y1''[t] == (\[Lambda]1[t]/Subscript[l, 1]) y1[t] - (\[Lambda]2[t]/Subscript[l, 2]) (y2[t] - y1[t]) - Subscript[m, 1] g,

   Subscript[m, 2] x2''[t] == (\[Lambda]2[t]/Subscript[l, 2]) (x2[t] - x1[t]),

   Subscript[m, 2] y2''[t] == (\[Lambda]2[t]/Subscript[l, 2]) (y2[t] - y1[t]) - Subscript[m, 2] g};

4、假设第一个摆长为l1，第二个摆长为l2：

ll = {x1[t]^2 + y1[t]^2 == Subscript[l, 1]^2, (x2[t] - x1[t])^2 + (y2[t] - y1[t])^2 == Subscript[l, 2]^2};

5、作为微分系统，需要有明确的初始状态：

begin={x1[0] == 1, y1[0] == 0, y1'[0] == 0, 

            x2[0] == 1, y2[0] == -1, y2'[0] == 0};

6、指定基本的物理参数：

pms = {g -> 9.81, Subscript[m, 1] -> 1, Subscript[m, 2] -> 1, Subscript[l, 1] -> 1, Subscript[l, 2] -> 1};

方程组、摆长固定、初始状态确定、物理参数明确，这个微分系统就具体化了，因此，可以对这个系统求数值解：

NDSolve[{fcz, ll, begin} /. pms, {x1, y1, x2, y2, λ1, λ2}, {t, 0, 15}]

7、这样就可以模拟双摆的摆动过程。

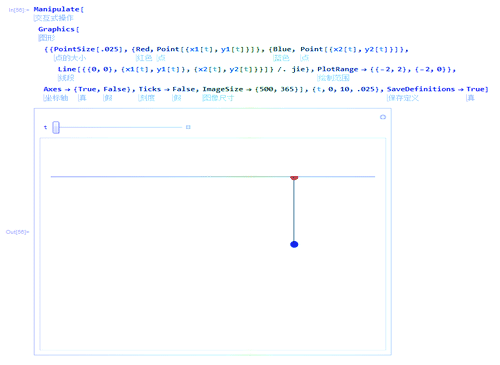
8、录制了一个动态图。

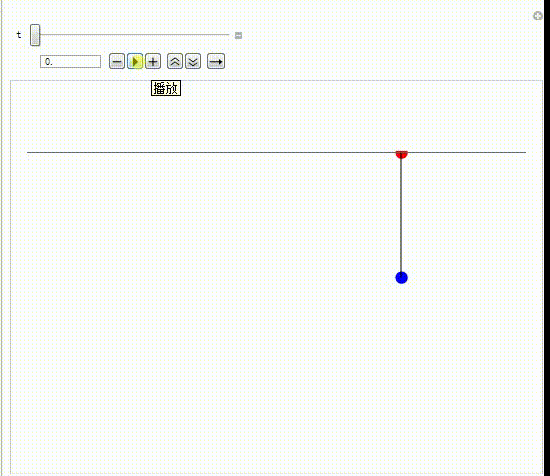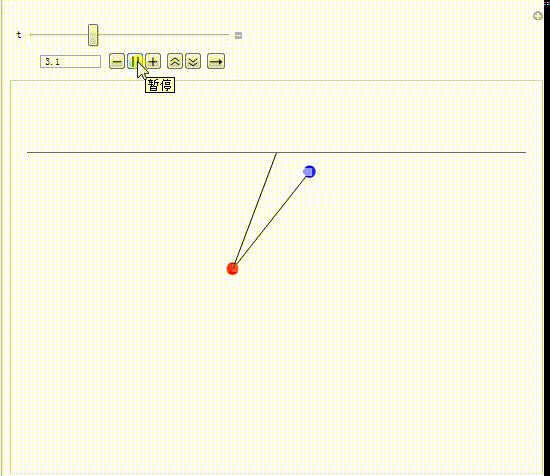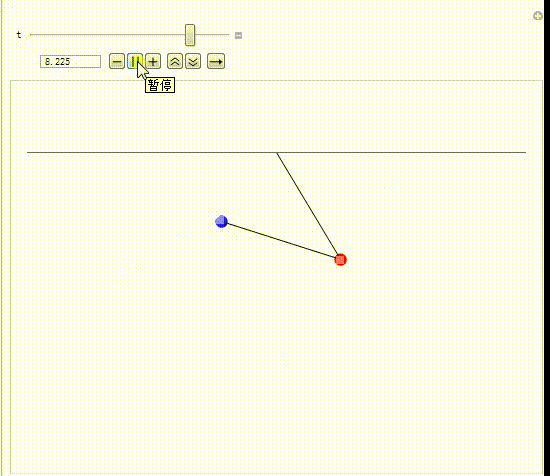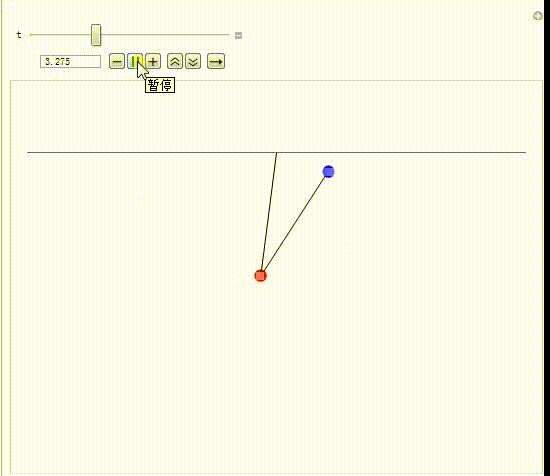
9、实时的画出第二个摆锤的移动轨迹。

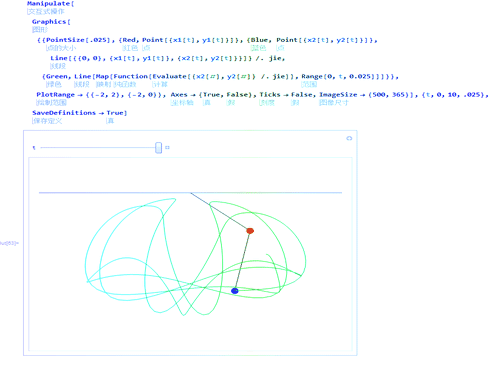
10、动态图。