解一元一次不等式六种类型应用举例思路方法之二

1、举例，当两个不等式解都为小于某个数时，则不等式组的解是这两某个数中的最小值。

2、当两个不等式解均为大于某个数时，则不等式组的解是这两某个数中的最大值，具体解答举例如下图所示。

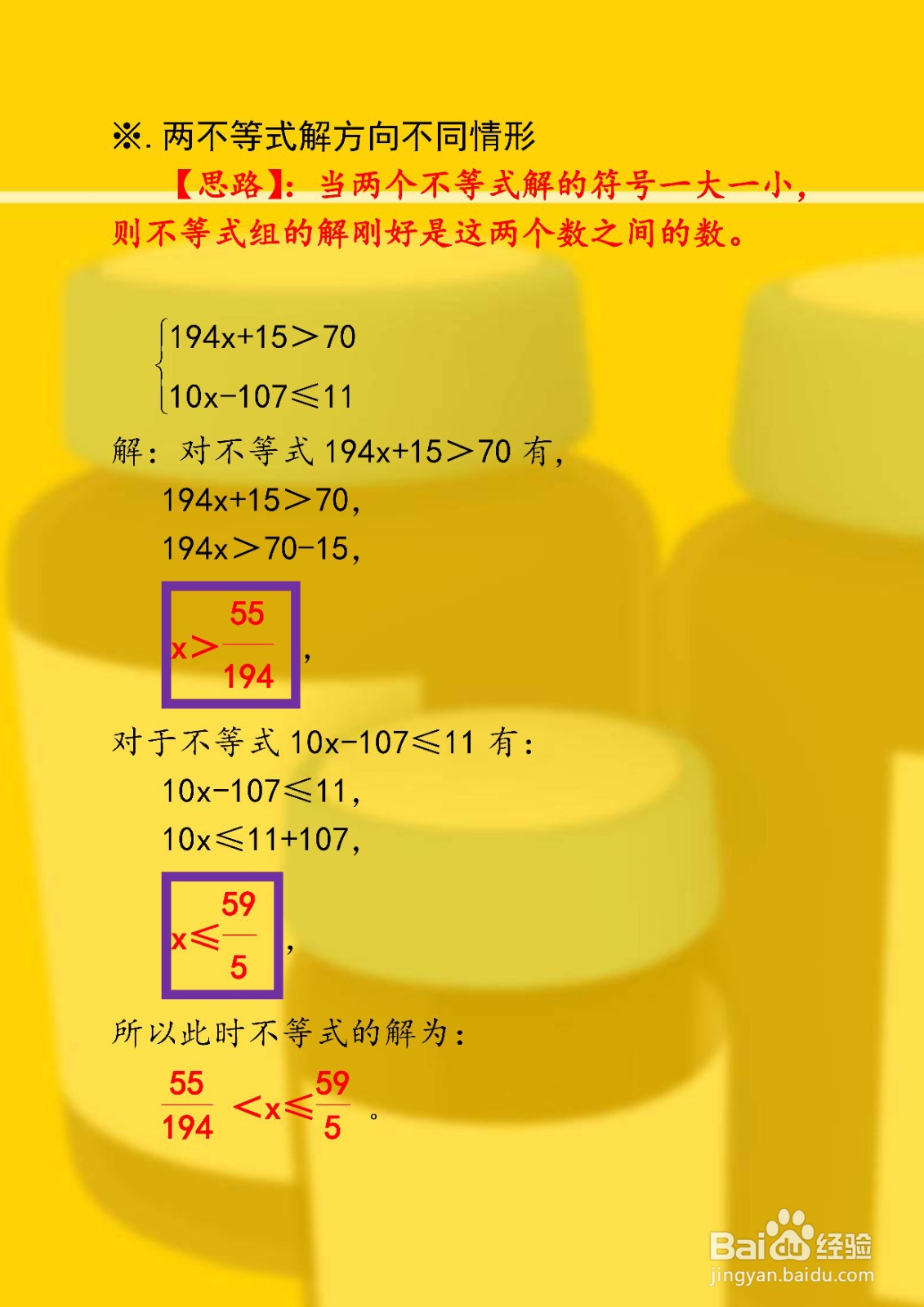
3、列举两不等式解方向不同情形，如194x+15>70，15x-107<11，则不等式组的解刚好是这两个数之间的数。

4、两不等式其一含有分式情形，【思路】：当两个不等式中一个含有分式时，则对该分式进行通分，再按不等式组解法进行求解。

5、解析两不等式中均含有分式情形，当两个不等式倦虺赳式中都含有分式时，则对分别对两分式进行通分，再按不等式组解法进行求解，详细举例如下图所示。

6、当不等式是两边夹时，实际是不等式组，既可以分别求解，也可以变形求解，本例-4≤（-2x+5）/26≤3是变形求解。