ForAll函数的用法（Mathematica）
1、x+1/x≥2，并不恒成立。
3、这种方法，可以用来证明二次均值不等式在全体实数范围内恒成立。
5、而三次均值不等式，需要数字全是正数，才能成立。
7、求对于任意实数x，a x^2+b x+c≥0恒成立，a、b、c所需要满足的条件。
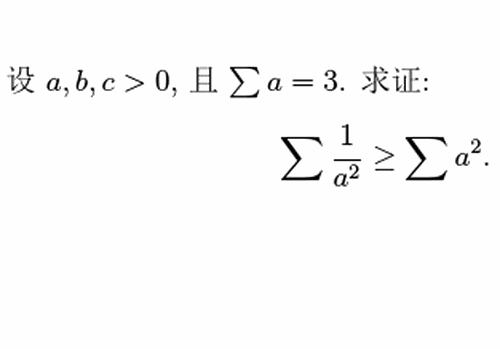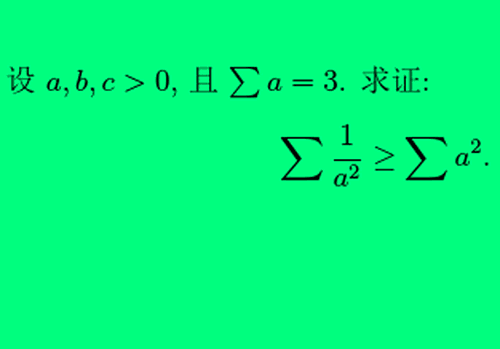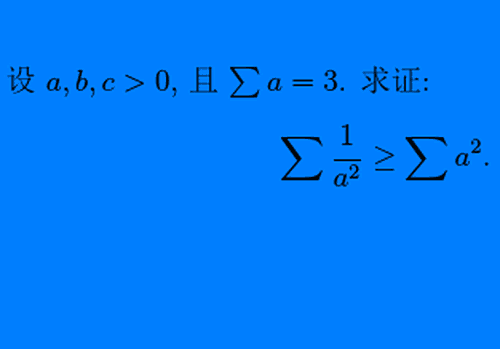
声明：本网站引用、摘录或转载内容仅供网站访问者交流或参考，不代表本站立场，如存在版权或非法内容，请联系站长删除，联系邮箱：site.kefu@qq.com。
阅读量：69
阅读量：85
阅读量：83
阅读量：55
阅读量：87