齐次线性方程组为什么当D=0时有非零解

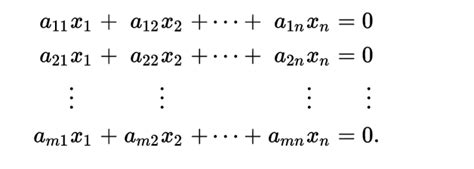
首先，你说反了。齐次线性方程组中，如果D≠0,则只有零解；如果有非零解,则系数行列式D=0。

这两个部分互为逆否命题,如果前半部分成立,则后半部分必然成立。

∵齐次线性方程组的常数项全为0,∴Dj=0

又∵D≠0

∴解xj=Dj/D=0,即所有解均等于0,即全为0解

这就证明了前半部分成立,因此后半部分也成立。

就是解不等于0。

齐次线性方程组，指常数项全部为零的线性方程组。

基本性质：

1.齐次线性方程组的两个解的和仍是齐次线性方程组的一组解。

2.齐次线性方程组的解的k倍仍然是齐次线性方程组的解。

3.齐次线性方程组的系数矩阵秩r(A)=n，方程组有唯一零解。

4.齐次线性方程组的系数矩阵秩r(A)<n，方程组有无数多解。

5. n元齐次线性方程组有非零解的充要条件是其系数行列式为零。

齐次线性方程组与非齐次线性方程组的区别：齐次的没有常数项，就是AX=0，非齐次的有常数项，就是AX=B。