如何用stata画图检验自相关？

1、首先，我们打开笔者准备 的数据集，然后观察对数据集进行初步的观察。

通过观察我们可以得知t是时间变量，第一步我们应该设定变量t为时间表示。

tsset t

2、我们对已有的数据进行回归

reg y x1 x2 x3

解释：对变量进行回归，在实际分析中仅需要将你想要分析的被解释变量和解释变量带入即可。

（图片是我举的例子）

3、如果实际应用中的数据是时间序列，那么有很大可能性存在自相关性，所以我绘制残差与残差滞后的散点图，来观察是否存在自相关性

predict e1,r

twoway scatter e1 L.e1 || lfit e1 L.e1

解释：1.选项r是residual，表示的是残差

2.twoway scatter表示的是画散点图，||表示的是并列画在一张图上，L.表示滞后，lfit表示的是linear fit，更多信息可以参考我的其他经验。

    通过观察，我们可以看出时间趋势与残差散点图存在相关关系，我们可以初步认为存在1阶正的自相关。

4、我们可以进一步画一下，二阶滞后的散点图

twoway scatter e1 L2.e1 || lfit e1 L2.e1

观察直线几乎是水平的，我们初步判断不存在2阶滞后的自相关。

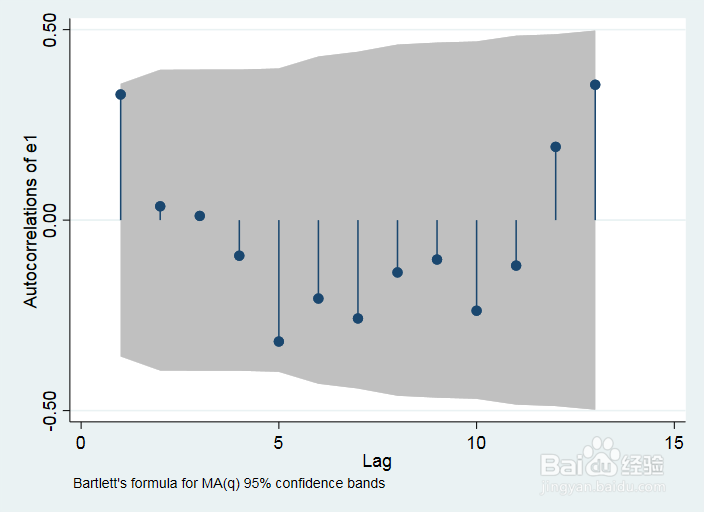
5、进一步地我们可以使用stata绘制残差的自相关图

ac e1

解释：1.ac代表的是autocorrelation

    通过观察自相关图我们看出，除了1阶自相关十分接近95%的置信区间，其他的都能够比较好的拒绝存在自相关这一原假设。其中灰色的区域表示的是自相关的置信区间。