在matlab中如何了解矩阵和幻方矩阵？

1、输入矩阵

开始学习 MATLAB 的最佳方法是了解如何处理矩阵。启动 MATLAB 并按照每个示例操作。

您可以采用多种不同方法在 MATLAB 中输入矩阵：

• 输入元素的明确列表。

• 从外部数据文件加载矩阵。

• 使用内置函数生成矩阵。

• 使用您自己的函数创建矩阵，并将其保存在文件中。

首先，以元素列表的形式输入丢勒的矩阵。您只需遵循一些基本约定：

• 使用空格或逗号分隔行的元素。

• 使用分号 ; 表示每行末尾。

• 使用方括号 [ ] 将整个元素列表括起来。

2、要输入丢勒矩阵，只需在命令行窗口中键入即可

A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1]

MATLAB 显示刚才您输入的矩阵：

3、矩阵求和、转置和对角矩阵

您可能已经注意到，幻方矩阵的特殊属性与元素的不同求和方法相关。如果沿任何行或列求和，或者沿两条主对角线中的任意一条求和，您将始终得到相同数字。让我们使用 MATLAB 来验证这一点。尝试的第一个语句是

sum(A)

MATLAB 返回的结果为

4、如果未指定输出变量，MATLAB 将使用变量 ans（answer 的缩略形式）来存储计算结果。您已经计算包含 A 的列总和的行向量。每个列的总和都相同，即幻数和 34。

行总和如何处理？MATLAB 会优先处理矩阵的列，因此获取行总和的一种方法是转置矩阵，计算转置的列总和，然后转置结果。

5、MATLAB 具有两个转置运算符。撇号运算符（例如，A'）执行复共轭转置。它会围绕主对角线翻转矩阵，并且还会更改矩阵的任何复数元素的虚部符号。点撇号运算符 (A.') 转置矩阵，但不会影响复数元素的符号。对于包含所有实数元素的矩阵，这两个运算符返回相同结果。

因此

A'

生成

6、而

sum(A')'

生成包含行总和的列向量

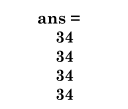
7、有关避免双重转置的其他方法，请在 sum 函数中使用维度参数：

sum(A,2)

生成

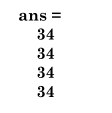
8、使用 sum 和 diag 函数可以获取主对角线上的元素的总和：

diag(A)

生成

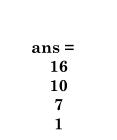
9、而

sum(diag(A))

生成

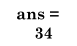
10、从数学上讲，另一条对角线（即所谓的反对角线）并不是十分重要，因此 MATLAB 没有对此提供现成的函

数。但原本用于图形的函数 fliplr 可以从左往右地翻转矩阵：

sum(diag(fliplr(A)))

11、magic 函数

MATLAB 实际包含一个内置函数，该函数可创建几乎任意大小的幻方矩阵。此函数称为 magic 也就不足

为奇了：

B = magic(4)

12、此矩阵几乎与丢勒雕刻中的矩阵相同，并且具有所有相同的“神奇”性质；唯一区别在于交换了中间两列。

您可以交换 B 的中间两列，使其看起来像丢勒 A。针对 B 中的每一行，按照指定顺序（1、3、2、4）对列进行重新排列：A = B(:,[1 3 2 4])

13、生成矩阵

MATLAB 软件提供了四个用于生成基本矩阵的函数。

zeros 全部为零

ones 全部为 1

rand 均匀分布的随机元素

randn 正态分布的随机元素

14、Z = zeros(2,4)

15、F = 5*ones(3,3)

16、N = fix(10*rand(1,10))

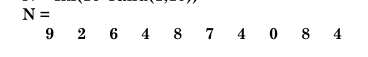
17、R = randn(4,4)