【Mathematica】怎么绘制三维复数图？

1、绘制图像：

ComplexPlot3D[z - Sin[z], {z, -2 - 2 I, 2 + 2 I}]

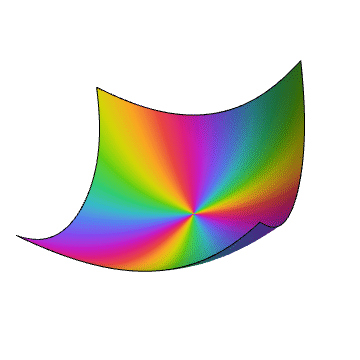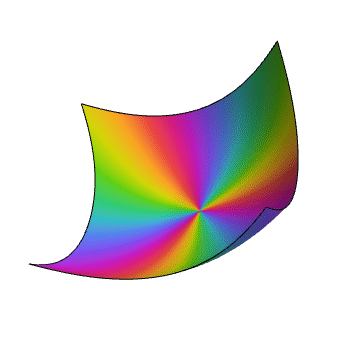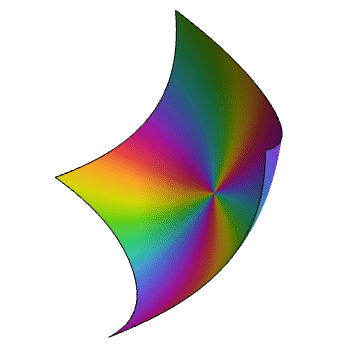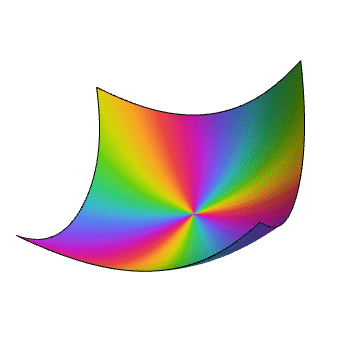
2、作图函数是一个单值的一元复函数：

ComplexPlot3D[Tan[z], {z, -2 - 2 I, 2 + 2 I}]

3、绘图范围是一个矩形区域，{z, -2 - 2 I, 2 + 2 I}表示的是：

实部在-2到2之间，虚部也在-2到2之间。

换一个画图范围：

ComplexPlot3D[Tan[Sin[z]], {z, -2 - 3 I, 2 + 3 I}]

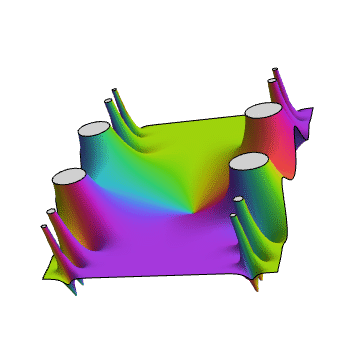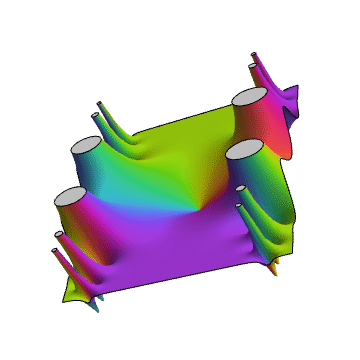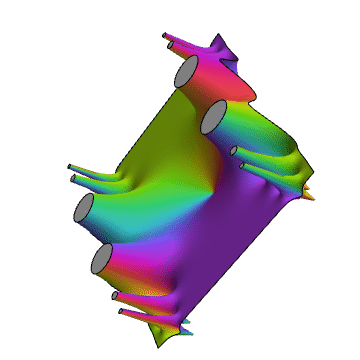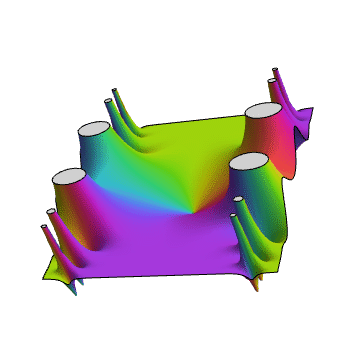
4、画图的曲面高度，以函数的模长为例，也就是说整个曲面一定位于复平面上方。

ComplexPlot3D[z^Sin[z] + 1/z, {z, -2 - 2 I, 2 + 2 I}]

5、默认的着色依据是函数值的辐角，其它着色方案需要另行指定：

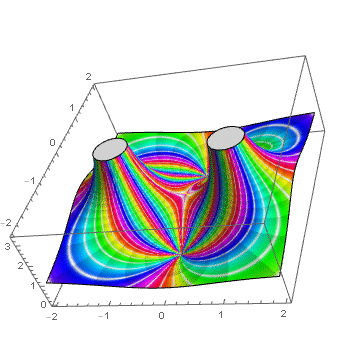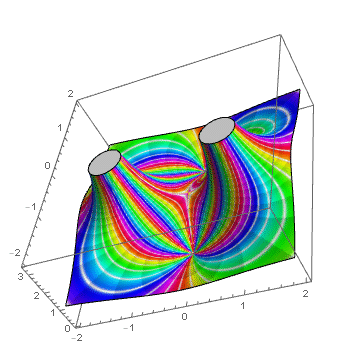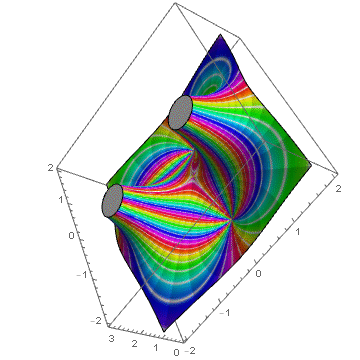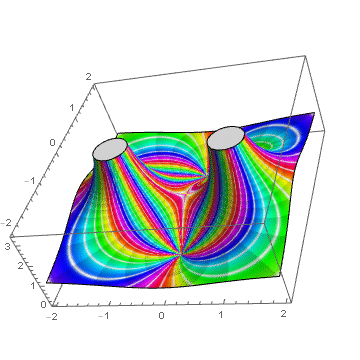
ComplexPlot3D[(z^2 + 1)/(z^2 - 1), {z, -2 - 2 I, 2 + 2 I}, 

 ColorFunction -> (Hue[#8, 1 - Cos[8 \[Pi] #8]^20, 

     1 - 0.2 SawtoothWave[6 #7]] &), ColorFunctionScaling -> False]

6、(z^3 + 1)/z^3：