【Mathematica】探索精确度对抛物线映射的影响

1、把抛物线迭代映射，写为如下的自定义函数：

f[x_, n_] :=  Floor[3.5*(10^n)* (1 - x) x]/(10.^n)

这样，既考虑了抛物线映射的迭代过程，又考虑了不同精度的结果。

其中，n是正整数，表示每一步都精确到小数点后n位数。

当n=1的时候，只保留小数点后一位数：

n = 1;

xx = NestList[f[#, n] &, N[1/Pi, n], 100]

这个时候，迭代过程迅速收敛。

2、n=2，保留小数点后两位数字：

n = 2;

xx = NestList[f[#, n] &, N[1/Pi, n], 100]

第六步之后，开始进入循环状态。

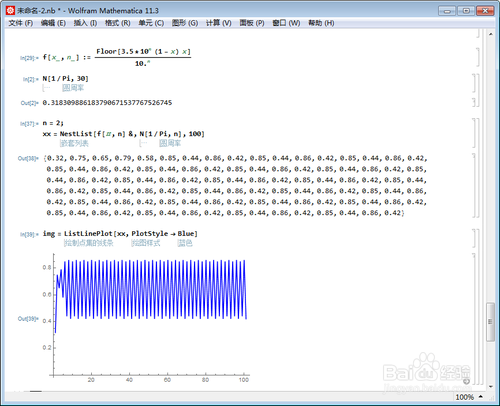
3、n=3，保留小数点后三位有效数字，则在第17步之后，才出现循环状态：

4、n=4，也是在第17步之后出现循环状态：

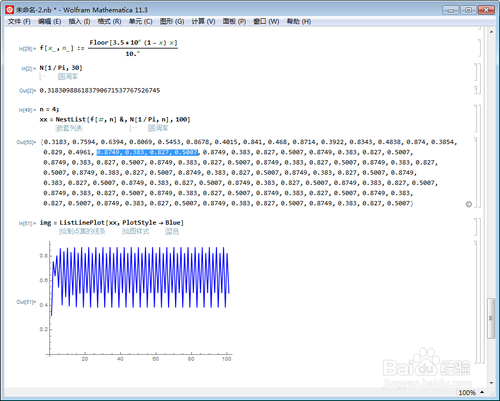
5、n=5，在第21步之后出现循环：

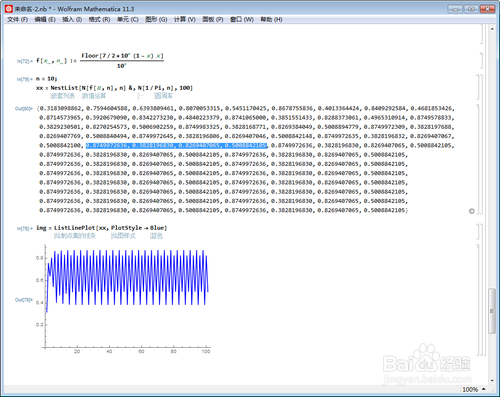
6、n=10，保留小数点后10位有效数字：

f[x_, n_] :=  Floor[7/2*10^n (1 - x) x]/10^n

n = 10;

xx = NestList[N[f[#, n], n] &, N[1/Pi, n], 100]

在第37步之后才出现循环状态。