beyes方法诞生于
1、Pr_omiga1=input('请输入第一类的先验概率:');
百度
Pr_omiga2=input('请输入第二类的先验概率:');
Num=20;
s1=mvnrnd([0 1],eye(2),Num)'
s2=mvnrnd([2 0],3*eye(2),Num)'
s11=s1(1,:);
s12=s1(2,:);
s21=s2(1,:);
s22=s2(2,:);
muGiven1=[0 1]';
sigmaGiven1=eye(2);

2、% 求正态分布条件下的基于最小错误率的Bayesian决策分类器的决策面
% 预求相关参量
W1 = -0.5 * inv(sigma1);
W2 = -0.5 * inv(sigma2)
omiga1= inv(sigma1) *
omiga1= inv(sigma1) *
omiga10= -0.5*mu1'*inv(sigma1)*mu1 -0.5*log(det(sigma1)) + log(Pr_omiga1)
;omiga20= -0.5*mu2'*inv(sigma2)*mu2 -0.5*log(det(sigma2)) + log(Pr_omiga2);
3、 //显示类标号属性
ListClass();
DataSet ds1=BindCredentialDropDwon();
this.DropDownList2.DataSource=ds1;
this.DropDownList2.DataTextField="CreditRating";
this.DropDownList2.DataValueField="CreditRating";
this.DropDownList2.DataBind();
4、 //先验概率的计算
FrontProbability(out FrontYesProbability, out FrontNoProbability);
string FrontYesProbility="p"+"(" + "IsBuyComputer="+ "/"yes/"" +")"+"="+FrontYesProbability;
string FrontNoProbility="p"+"(" + "IsBuyComputer="+ "/"no/"" +")"+"="+FrontNoProbability;
5、 //收入的条件概率的计算
float pIncome=0;
float _pIncome=0;
pFrontCalculate(out pIncome,out _pIncome,"Income","high");
string IncomeFrontYesProbility="p"+"(" + "Income="+ "/"high/"" +"|"+"IsBuyComputer="+ "/"yes/""+")"+"="+pIncome;
string IncomeFrontNoProbility="p"+"(" + "Income="+ "/"high/"" +"|"+"IsBuyComputer="+ "/"no/""+")"+"="+_pIncom
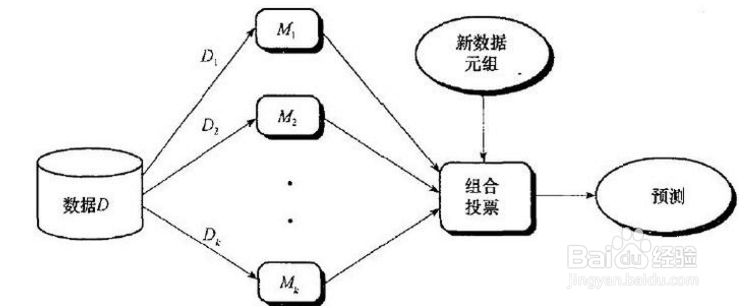
1、1.详细介绍了贝叶斯公式在自动文本分类领域的使用,并且提到了关于互信息特征提取的方法。
2.贝叶斯网络使用图形的方法描述数据间的相互关系,语义清晰,易于理解。
3.图形化的知识表示方法使得保持概率知识库的一致性和完整性变得容易,可以方便地针对条件的改变进行网络模块的重新配置。