在平面中,一个点绕任意点旋转θ度后的点的坐标
1、证:设点(x0,y0)到点(rx0,ry0)的距离为La,点(x,y)到点(rx0,ry0)的距离为Lb
则由图1可得:
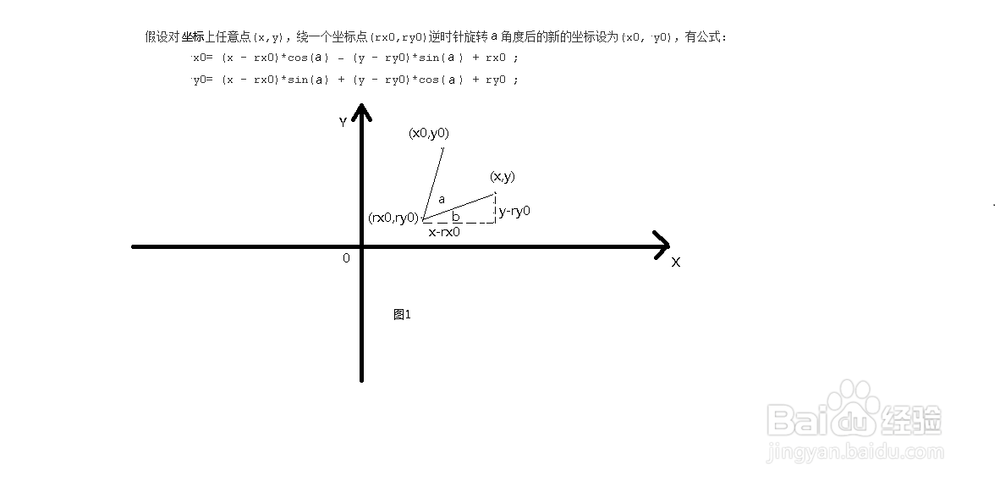
2、( x0 - rx0 ) / La = cos(a + b) - ①
( x - rx0 ) / Lb = cos(b) - ②
La = Lb - ③
( y0 - ry0 ) / La = sin(a+b) - ④
( y - ry0 ) / Lb = sin(b) - ⑤
当cos(b),cos(a + b)不为零时,由①②③得:
(x0- rx0)/ (x-rx0) = cos(a+b)/cos(b)
(x0- rx0)/ (x-rx0) = (cos(a)cos(b)-sin(a)sin(b))/cos(b)
(x0- rx0)/ (x-rx0) = cos(a) - sin(a)tan(b)
(x0- rx0) = (cos(a) - sin(a)tan(b))(x - rx0)
x0 = (x - rx0)cos(a) - sin(a)tan(b)(x - rx0) + rx0
x0 = (x - rx0)cos(a) - (y - ry0)sin(a) + rx0 - A
当sin(b),sin(a + b)不为零时,由③④⑤得:
(y0 - ry0)/(y - ry0) = sin(a+b)/sin(b)
(y0 - ry0)/(y - ry0) = (sin(a)cos(b) + cos(a)sin(b))/sin(b)
(y0 - ry0)/(y - ry0) = sin(a)cos(b)/sin(b) + cos(a)
y0 = (y - ry0)sin(a)cos(b)/sin(b) + (y - ry0)cos(a) + ry0
y0 = (y - ry0)sin(a)(x - rx0)/(y - ry0) + (y - ry0)cos(a) + ry0
y0 = (x - rx0)sin(a) + (y - ry0)cos(a) + ry0 - B
∴当cos(b),cos(a + b)不为零时A、B式成立
3、 当cos(a+b)= 0时,即x0 = rx0,a+b = π/2+kπ(k>=0的自然数)如图2:
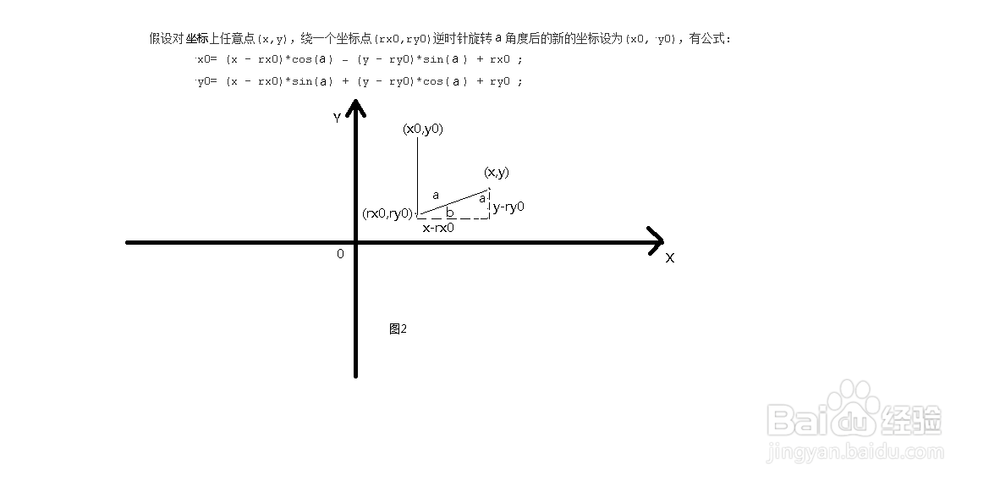
4、∵cos(a+b)= 0
cos(a)cos(b) - sin(a)sin(b) = 0
tan(a) = 1/tan(b)
sin(a)/cos(a) = (x - rx0)/(y - ry0)
(x - rx0)cos(a) = (y - ry0)sin(a)
将x0 = rx0式代入A式也得
(x - rx0)cos(a) = (y - ry0)sin(a)
∴当cos(a+b)= 0时A式成立。
5、 ∵tan(a) = (x - rx0)/(y - ry0) - ⑥
La = Lb = y0 - ry0 - ⑦
由⑥得
(y - ry0)sin(a)/cos(a) = (x - rx0)
(y - ry0)sin²(a)/cos(a) = (x - rx0)sin(a)
(y - ry0)(1-cos²(a))/cos(a) = (x - rx0)sin(a)
(y - ry0)(1/cos(a)-cos(a)) = (x - rx0)sin(a)
(y - ry0)/cos(a)-(y - ry0)cos(a)) = (x - rx0)sin(a)
(y - ry0)/cos(a) = (x - rx0)sin(a) +(y - ry0)cos(a)) - ⑧
由⑦得
(y - ry0)/cos(a) = (x - rx0)/sin(a) = y0 - ry0
y0 = (y - ry0)/cos(a) + ry0 - ⑨
将⑧代入⑨得:
y0 = (x - rx0)sin(a) +(y - ry0)cos(a) + ry0
∴当cos(a+b)= 0时B式成立。
6、 当sin(a) = 0时,即a = π/2+ kπ(k>=0的自然数)如图3所示:
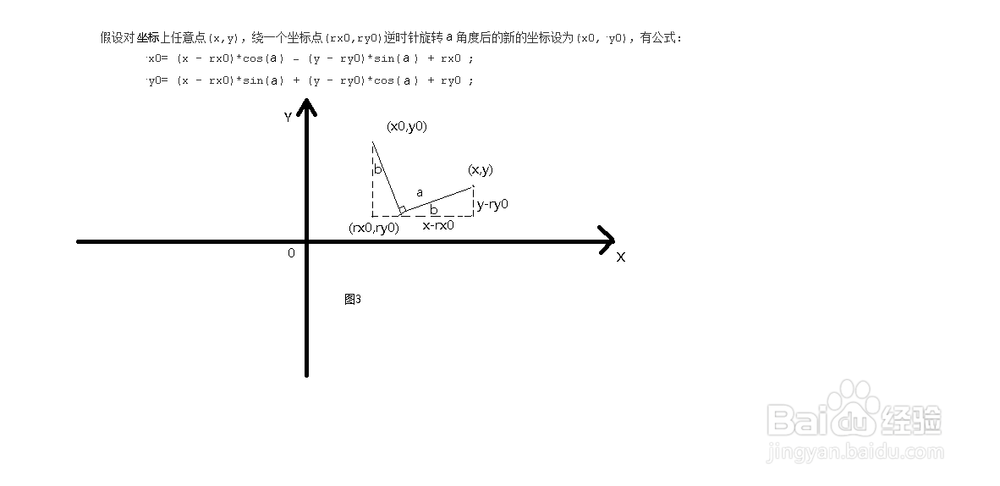
7、∵sin(b) = (x0 - rx0)/La = (y - ry0)/Lb
cos(b) = (y0 - ry0)/La = (x - rx0)/Lb
即:
x0 - rx0 = y - ry0
y0 - ry0 = x - rx0
得:
x0 = y - ry0 + rx0
y0 = x - rx0 + ry0
把a= π/2+ kπ代入A、B两式得:
x0 = y - ry0 + rx0
y0 = x - rx0 + ry0
∴当sin(a) = 0时,A、B两式也成立
8、 当cos(b)= 0时,即x = rx0,b = π/2 +kπ(k>=0的自然数)如图4:
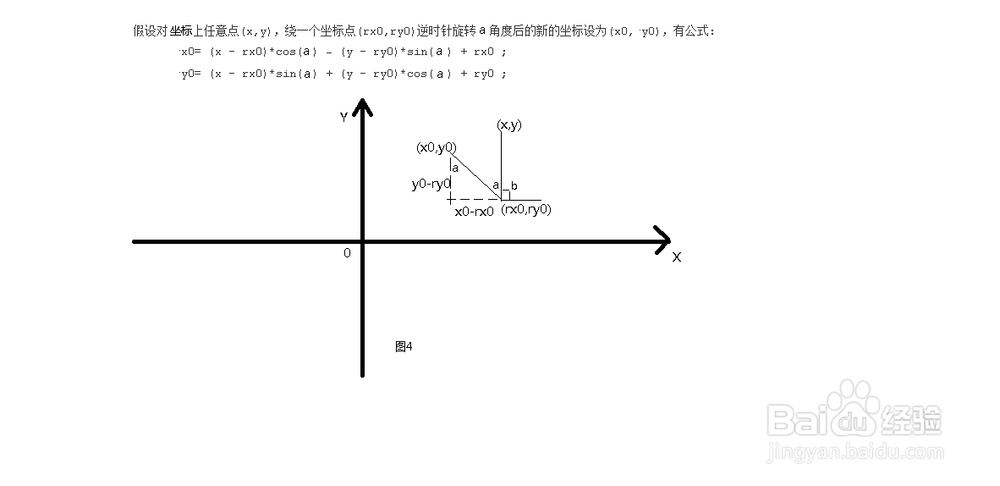
9、∵La = Lb = y - ry0 - ⑴
sin(a)= ( x0 - rx0 ) / La - ⑵
cos(a)= ( y0 - ry0 ) / La - ⑶
由⑴⑵⑶得:
x0 = (y - ry0)sin(a)+ rx0
y0 = (y - ry0)cos(a)+ ry0
将b = π/2+kπ 代入A、B两式也得
x0 = (y - ry0)sin(a)+ rx0
y0 = (y - ry0)cos(a)+ ry0
∴当cos(b)= 0时,符合A、B两式。
10、 当sin(a+b) = 0时,即y0 = ry0,a+b = π+kπ(k>=0的自然数),如图5所示:

11、∵sin(a+b) = 0
∴sin(a)cos(b) + cos(a)sin(b) = 0
tan(a) + tan(b) = 0
sin(a)/cos(a) + (y - ry0)/(x - rx0) = 0
(x - rx0)sin(a) + (y - ry0)cos(a) = 0
将y0 = ry0 代入B式也得:
(x - rx0)sin(a) + (y - ry0)cos(a) = 0
∴当sin(a+b)= 0时A式成立。
12、 ∵tan(a) = tan(π- b) = - tan(b) = -(y - ry0)/(x - rx0) - ⑷
La = Lb = rx0 - x0 - ⑸
由 ⑷ 得:
tan(a) = -(y - ry0)/(x - rx0)
(x - rx0)sin(a)/cos(a) = -(y - ry0)
(x - rx0)sin²(a)/cos(a) = -(y - ry0)sin(a)
(x - rx0)(1-cos²(a))/cos(a) = -(y - ry0)sin(a)
(x - rx0)/cos(a)-(x - rx0)cos(a) = -(y - ry0)sin(a)
(x - rx0)/cos(a) = (x - rx0)cos(a)-(y - ry0)sin(a) - ⑹
由 ⑸ 得:
(y - ry0)/sin(b) = (x - rx0)/cos(b) = rx0 - x0
x0 = rx0 - (x - rx0)/cos(b)
x0 = rx0 - (x - rx0)/cos(π-a)
x0 = rx0 + (x - rx0)/cos(a) - ⑺
把 ⑹ 代入 ⑺ 得:
x0 = (x - rx0)cos(a)-(y - ry0)sin(a) + rx0
∴当sin(a+b)= 0时B式成立。
13、
综上所述,对图片上任意点(x,y),绕一个坐标点(rx0,ry0)逆时针旋转a角度后的新的坐标设为(x0, y0),有公式:
x0= (x - rx0)*cos(a) - (y - ry0)*sin(a) + rx0 ; y0= (x - rx0)*sin(a) + (y - ry0)*cos(a) + ry0 ;