如何画分式函数y=(2x³-4)/(x+1)³的图像示意图?
1、函数是分式函数,根据函数特征,分母应不为0,即可得到不等式x+1≠0,则可计算出函数的定义域。

2、 在高中数学里,定义域的定义为:设A,B是两个非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A--B为集合A到集合B的一个函数,记作y=f(x),x属于集合A。其中,x叫作自变量,x的取值范围A叫作函数的定义域。
1、 利用函数的导数知识,计算函数的一阶导数,根据导数的符号,解析函数y的单调性。
2、 函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。

1、计算函数的二阶导数,即可求出函数的拐点,进而解析函数单调性,则可求出函数的凸凹区间。


2、拐点,又称反曲点,在数学上指改变曲线向上或向下方向的点,直观地说拐点是使切线穿越曲线的点(即连续曲线的凹弧与凸弧的分界点)。若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处异号(由正变负或由负变正)或不存在。
1、计算函数在无穷远处和函数的点断点处的极限:
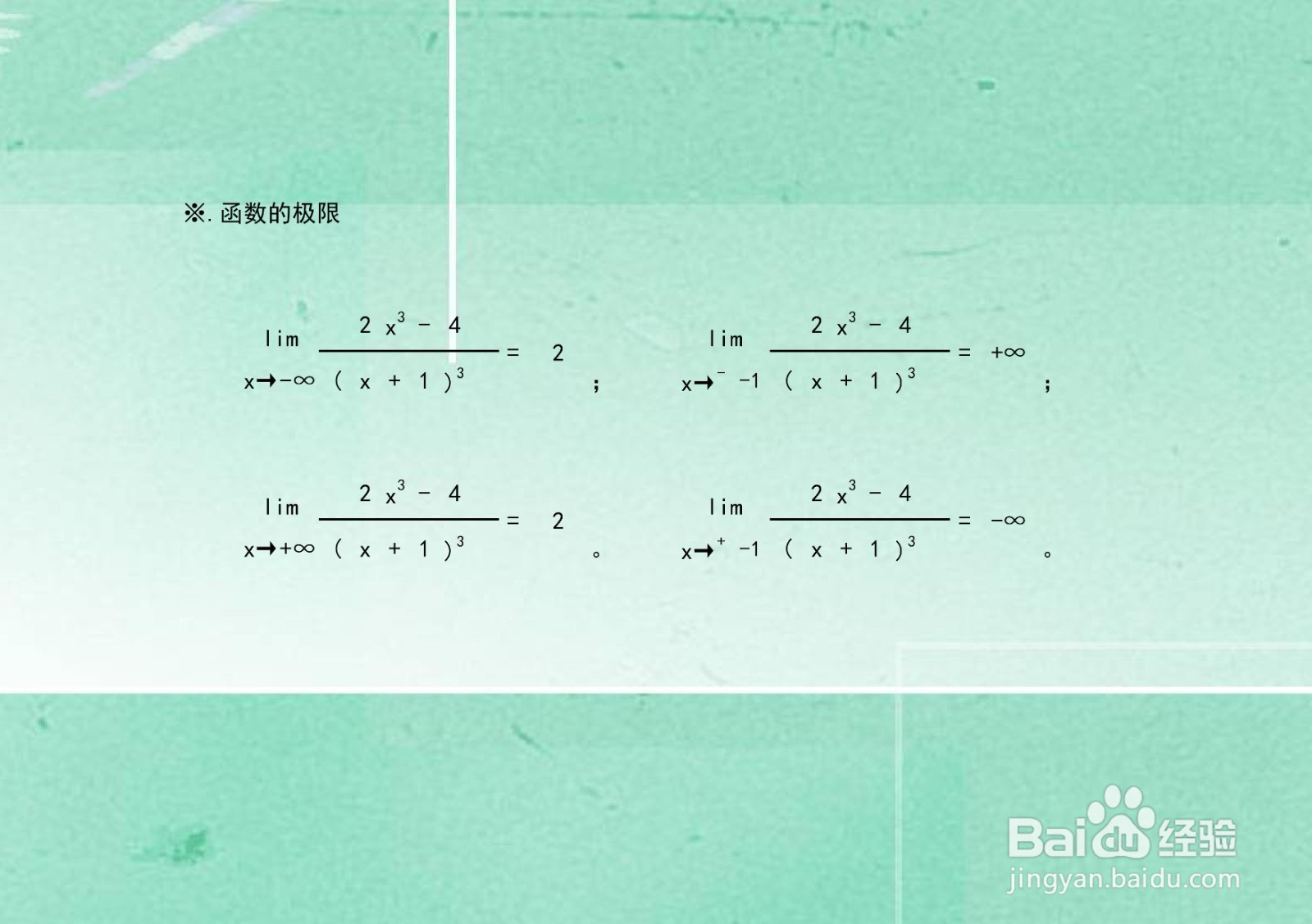
1、根据函数单调性、凸凹性等性质,列举函数在定义域区间上部分关键点坐标。
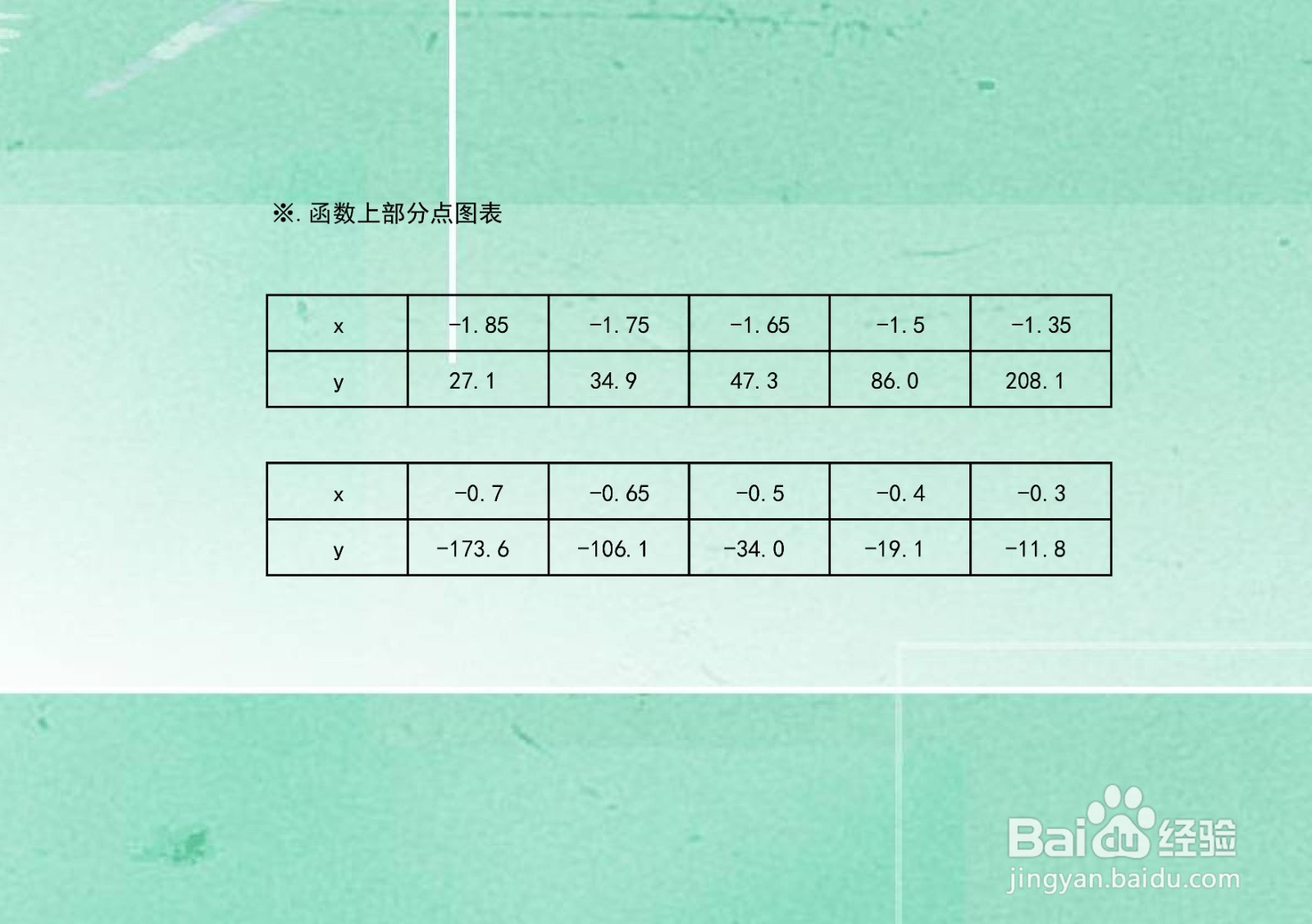
2、函数上部分点坐标的解析,是通过二维坐标系画函数图像的关键步骤。
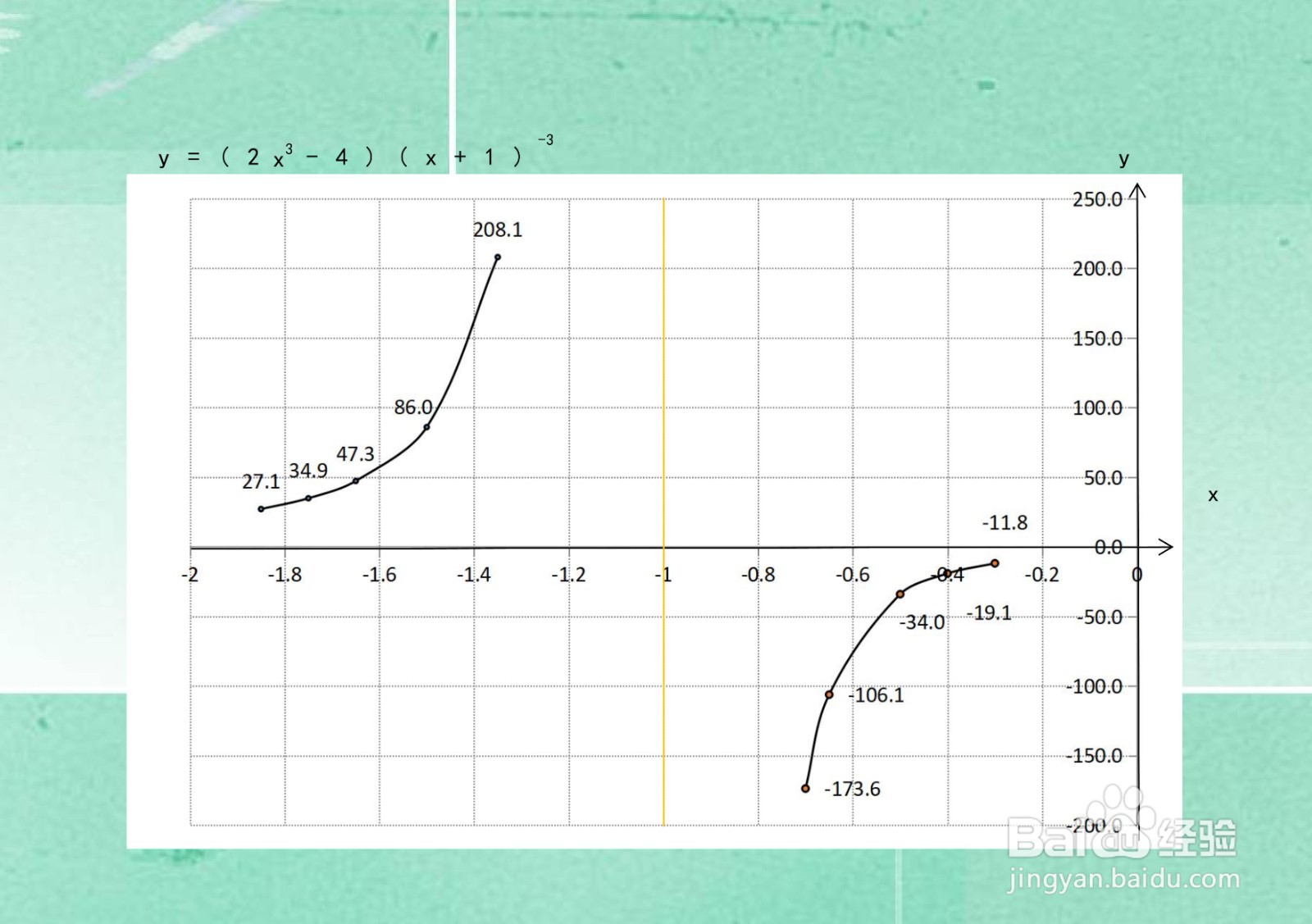
3、综合以上函数的定义域、单调性、凸凹性、极限性质,并结合函数的定义区间和单调、凸凹区间,即可画出函数的示意图如下:
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:43
阅读量:135
阅读量:46
阅读量:61
阅读量:23