姿态解算常用的知识

1、导航坐标系: 即地球坐标系,地理坐标系,也就是用东北地作为X,Y,Z轴建立起来的坐标系.(习惯上称为n系)

机体坐标系:也就是惯导固定的载体.实际上这里的飞机和惯导是相互固连的,机体坐标系也就是惯导的坐标系.(习惯上称为b系)

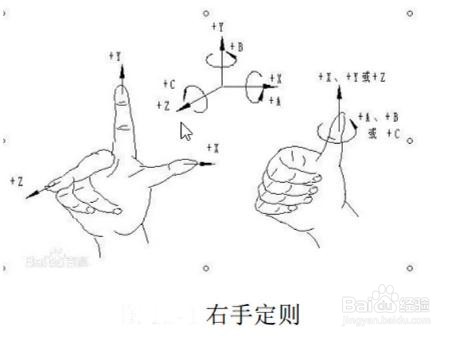
惯导满足右手定则,右手定则有两个含义:

一方面是用右手可以确定惯导坐标系的XYZ轴.

另一方面是,可以用右手确定各个轴的角速度方向.

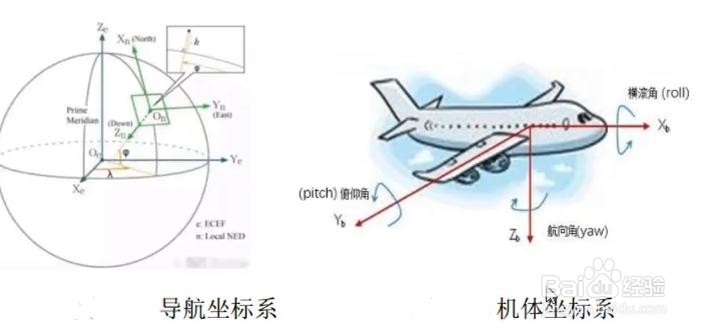
2、姿态:比如飞行器的俯仰,横滚,航向等角度. 姿态有什么用呢?知道了这些我们可以让飞行器做出翻滚,还可以用于控制飞行方向.

在四旋翼中,姿态就是人站在平地上,以平地为参考,观察四旋翼的各个轴的倾角.

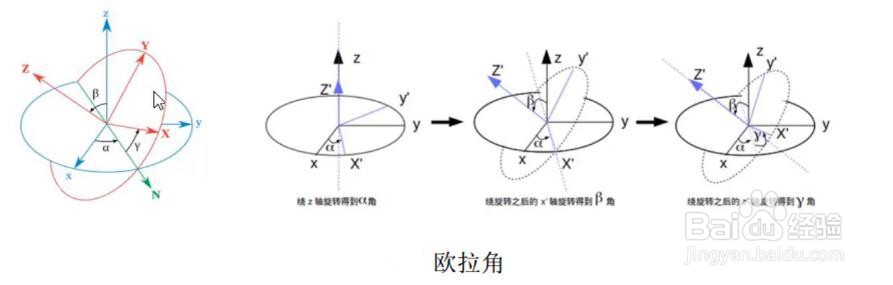
姿态的表示方式有:四元数,欧拉角和方向余弦矩阵.如果想要深入研究,这些知识需要十分了解.

下图是欧拉角,表示的姿态.利用欧拉角表示姿态的好处是很直观.任意的姿态可以拆分成按照三个轴分别转动的组合.

3、四元数表达方式:矢量式,复数式,三角式,指数式,矩阵式.

其中的三角式和矩阵式在姿态推导中会用到.

还要学习一写基本的四元数运算.

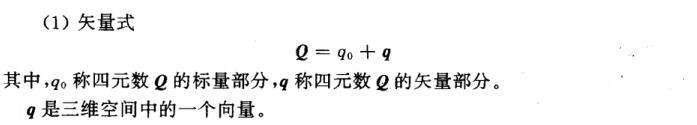
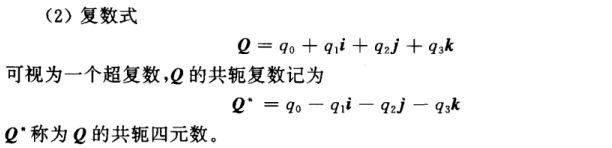
4、在某一时刻T1,四旋翼处于姿态1中;

经过一段时间,到达T2时刻,四旋翼处于姿态2中;

由姿态1过渡到姿态2可以用一个矩阵表达,(矩阵在某种程度上就是坐标变换),

[矩阵]*姿态1=姿态2     (这里是左乘矩阵)

这里的矩阵就是赫赫有名的: 坐标变换矩阵,或  余弦矩阵,或  方向余弦矩阵.

5、这个矩阵由两种表达形式,分别为欧拉角和四元数:

通过求解这个矩阵,就能够掌握四旋翼的实时动态.

欧拉角的表示方法虽然直观,易于理解,但是矩阵里面都是三角函数,计算起来比较复杂,导致实时响应低.所以先用了四元数的方式.

两者形式不一样,但是内容是一致的,且可以相互转换,推导繁琐,推导过程可以参考秦永元的书.

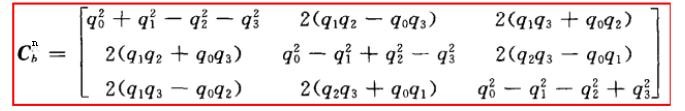
6、矩阵选用了四元数表达形式,那么问题来了.

怎么求取四元数呢?

这里要用到微分方程.用到了四元数的三角形式.

先看一下我们已知哪些参数,未知哪些参数:

[矩阵]*姿态1=姿态2

在上面式子中,姿态1我们是知道的.(这里是初始姿态,用的是四元数表达)

姿态2我们是不知道的.

[矩阵]是我们要求的. 矩阵里面都是四元数. 

(求出了矩阵,就能掌握姿态变化,矩阵式姿态变化的数学描述)

矩阵的组成主要用到了四元数,所以求矩阵,就是求四元数,用微分求解四元数.

(一节龙格库塔法)

如下图:

上一周期是姿态1,是已知的.

本周期是不知道的.

里面的w,是可以用陀螺仪测出来的.

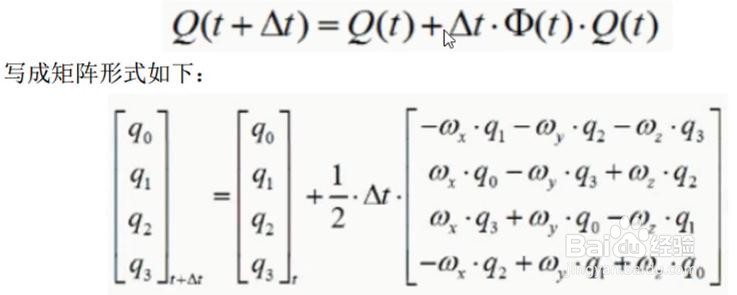
7、从上一步就可以求出来了.问题解决.

不过还有一个问题是如何保证陀螺仪测得的数据是准确的,

这里就用到了Mahony滤波算法.