Java 学习之经典算法(一)
1、1.河内之塔
河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数家 Edouard Lucas曾提及这个故事,据说创世纪时Benares有一座波罗塔,是由三支钻石棒(Pag)所支撑,开始时神在第一根棒上放置64个由上至下依由小至大排列的金盘(Disc),并命令僧侣将所有的金盘从第一根石棒移至第三根石棒,且搬运过程中遵守大盘子在小盘子之下的原则,若每日仅搬一个盘子,则当盘子全数搬运完毕之时,此塔将毁损,而也就是世界末日来临之时。
解法如下:
如果柱子标为ABC,要由A搬至C,在只有一个盘子时,就将它直接搬至C,当有两个盘子,就将B当作辅助柱。如果盘数超过2个,将第三个以下的盘子遮起来,就很简单了,每次处理两个盘子,也就是:A->B、A ->C、B->C这三个步骤,而被遮住的部份,其实就是进入程式的递回处理。事实上,若有n个盘子,则移动完毕所需之次数为2^n - 1,所以当盘数为64时,则n=64。如果对这数字没什幺概念,就假设每秒钟搬一个盘子好了,也要约5850亿年左右。
以下实例演示了 Java 河内之塔的实现:
public class MainClass {
public static void main(String[] args) {
int nDisks = 3;
doTowers(nDisks, 'A', 'B', 'C');
}
public static void doTowers(int topN, char from,char inter, char to) {
if (topN == 1){
System.out.println("盘子 1 从 "+ from + " 到 " + to);
}else {
doTowers(topN - 1, from, to, inter);
System.out.println("盘子 "+ topN + " 从 " + from + " 到 " + to);
doTowers(topN - 1, inter, from, to);
}
}
}
运行结果如下图:
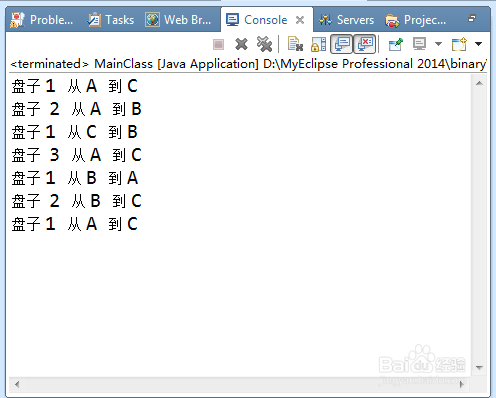
2、2. 费式数列
斐波那契数列指的是这样一个数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368……
特别指出:第0项是0,第1项是第一个1。
这个数列从第三项开始,每一项都等于前两项之和。
以下实例演示了 Java 斐波那契数列的实现:
public class MainClass {
public static long fibonacci(long number) {
if ((number == 0) || (number == 1))
return number;
else
return fibonacci(number - 1) + fibonacci(number - 2);
}
public static void main(String[] args) {
for (int counter = 0; counter <= 10; counter++) {
System.out.printf("斐波那契数列 of %d is: %d\n", counter,fibonacci(counter));
}
}
}
运行结果如下图:

3、3. 巴斯卡三角形
巴斯卡(Pascal)三角形基本上就是在解 nCr ,因為三角形上的每一個數字各對應一個nCr,其中 n 為 row,而 r 為 column,如下:
0C0 1C0 1C1 3C0 3C1 3C2 3C3 4C0 4C1 4C2 4C3 4C4
以下实例演示了 Java 巴斯卡三角形的实现:
public class MainClass {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
System.out.println("请输入巴斯卡三角行数:");
int num = scanner.nextInt();
pascalAssemble(num);
}
public static void pascalAssemble(int num){
int[][] value = new int[num][num];
for(int i = 0; i < num ;i++){
value[i][0] = 1;
value[i][i] = 1;
if(i > 1){
for(int j = 1; j < i ;j++){
value[i][j] = value[i-1][j-1] + value[i-1][j];
}
}
}
for(int i = 0; i < num ;i++){
for(int k = 0; k <= num - i;k++){
System.out.print(" ");
}
for(int j = 0; j<= i ;j++){
System.out.print(value[i][j]+" ");
}
System.out.println();
}
}
}
运行结果如下图:

4、4. 三色棋
问题说明:
三色旗的问题最早由E.W.Dijkstra所提出,他所使用的用语为Dutch Nation Flag(Dijkstra为荷兰人),而多数的作者则使用Three-Color Flag来称之。假设有一条绳子,上面有红、白、蓝三种颜色的旗子,起初绳子上的旗子颜色并没有顺序,您希望将之分类,并排列为蓝、白、红的顺序,要如何移动次数才会最少,注意您只能在绳子上进行这个动作,而且一次只能调换两个旗子。
解法
在一条绳子上移动,在程式中也就意味只能使用一个阵列,而不使用其它的阵列来作辅助,问题的解法很简单,您可以自己想像一下在移动旗子,从绳子开头进行,遇到蓝色往前移,遇到白色留在中间,遇到红色往后移。只是要让移动次数最少的话,就要有些技巧。
以下实例演示了 Java 三色棋的实现:
public class MainClass {
private void swap(char[] flags, int x, int y) {
char temp;
temp = flags[x];
flags[x] = flags[y];
flags[y] = temp;
}
public String move(char[] flags) {
int wFlag = 0;
int bFlag = 0;
int rFlag = flags.length - 1;
while (wFlag <= rFlag) {
if (flags[wFlag] == 'W') {
wFlag++;
} else if (flags[wFlag] == 'B') {
swap(flags, bFlag, wFlag);
bFlag++;
wFlag++;
} else {
while (wFlag < rFlag && flags[rFlag] == 'R')
rFlag--;
swap(flags, rFlag, wFlag);
rFlag--;
}
}
return new String(flags);
}
public static void main(String[] args) throws IOException {
BufferedReader buf = new BufferedReader(new InputStreamReader(System.in));
System.out.print("输入三色的顺序(例如: RWBBWRWR):");
String flags = buf.readLine();
MainClass threeColorsFlag = new MainClass();
flags = threeColorsFlag.move(flags.toUpperCase().toCharArray());
System.out.println("移动后的顺序为:" + flags);
}
}
运行结果如下图:

5、15. Eratosthenes 筛选求质数
说明:
除了自身之外,无法被其它整数整除的数称之为质数,在自然数中,除了1和此整数自身外,不能够被其他自然数整除的数,称之为质数。要求质数很简单,但如何快速的求出质数则一直是程式设计人员与数学家努力的课题,在这边介绍一个着名的Eratosthenes求质数方法。
解法:
首先知道这个问题可以使用回圈来求解,将一个指定的数除以所有小于它的数,若可以整除就不是质数,然而如何减少回圈的检查次数?如何求出小于N的所有质数?
首先假设要检查的数是N好了,则事实上只要检查至N的开根号就可以了,道理很简单,假设A*B = N,如果A大于N的开根号,则事实上在小于A之前的检查就可以先检查到B这个数可以整除N。不过在程式中使用开根号会精确度的问题,所以可以使用i*i <= N进行检查,且执行更快。
再来假设有一个筛子存放1~N,例如:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 ........ N
先用2的去做筛选,从4=22 开始,筛去2的倍数,循环步长为2: 2 3 5 7 9 11 13 15 17 19 21 ........ N
再用3的去做筛选,从9=32 开始,筛去3的倍数,循环步长为3: 2 3 5 7 11 13 17 19 ........ N
再用5的去做筛选,再用5的去做筛选,再用11的去做筛选........,如此进行到最后留下的数就都是质数,这就是Eratosthenes筛选方法(Eratosthenes Sieve Method)。
代码如下:
public class MainClass {
public static void main(String[] args) {
int N = 100;
int i = 0, j = 0, count = 0;
int prime[] = new int[N + 1];
// 初始化数据
for (i = 2; i <= N; i++) {
prime[i] = 1;
}
// 循环1(N 开方 次)
for (i = 2; i * i <= N; i++) {
if (prime[i] == 0) {
count++;
continue;
}
// 循环2(N/i 次) 筛选被i整除的数
for (j = i * i; j <= N; j = j + i) {
prime[j] = 0;
count++;
}
}
System.out.println("计算次数: " + count);
j = 0;
for (i = 2; i <= N; i++) {
if (prime[i] == 1) {
System.out.print("\t");
System.out.print(i);
j++;
if (j % 5 == 0) {
System.out.println();
}
}
}
}
}
