MATLAB求椭圆与直线的交点

1、第一，利用MATLAB求下图椭圆方程x^2/5^2+y^2/4^2=1和直线方程y=2*x+1的交点。

2、第二，启动MATLAB，新建脚本（Ctrl+N），在脚本编辑区输入如下代码：

close all; clear all; clc

syms x y

s=solve(x^2/5^2+y^2/4^2==1,y==2*x+1,x,y)

X=double(s.x)

Y=double(s.y)

3、第三，保存和运行上述脚本，在命令行窗口返回如下结果：

X =

    1.4179

   -2.2800

Y =

    3.8358

   -3.5599

也就是说，椭圆方程x^2/5^2+y^2/4^2=1和直线方程y=2*x+1的有两个交点，分别为（1.4179，3.8358）和（-2.2800，-3.5599）。

4、第四，在上述脚本的基础上，绘制椭圆方程x^2/5^2+y^2/4^2=1和直线方程y=2*x+1的图像，并标出两者的交点。在脚本编辑区接着输入如下代码：

h1=ezplot(x^2/5^2+y^2/4^2==1);

set(h1,'color',[0,0,0],'LineWidth',2)

axis equal;hold on;

h2=ezplot(y==2*x+1);

set(h2,'color',[0,0,1],'LineWidth',2)

legend('x^2/5^2+y^2/4^2==1','y==2*x+1',2)

plot(X,Y,'r.','MarkerSize',20)

text(X(1),Y(1),'(1.4179, 3.8358)','FontSize',15)

text(X(2),Y(2),'(-2.2800, -3.5599)','fontsize',15)

plot(0,[-10:0.01:10],'k');plot([-10:0.01:10],0,'k')

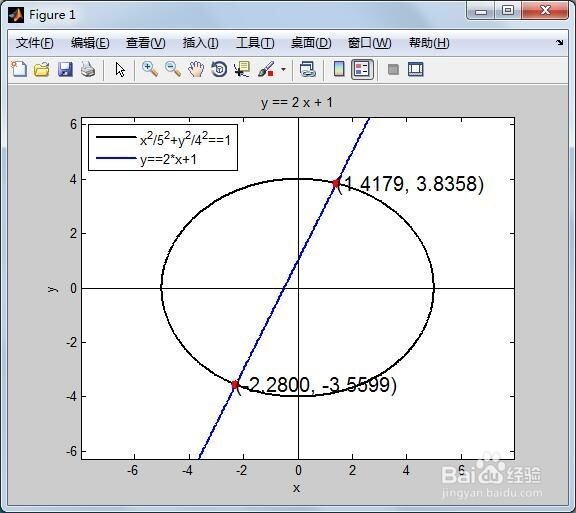
5、第五，保存和运行上述改进后的脚本，得到椭圆方程x^2/5^2+y^2/4^2=1和直线方程y=2*x+1的图像，并标出两者的交点（1.4179，3.8358）和（-2.2800，-3.5599）。