怎么使用Mathematica——AnglePath

1、AnglePath[{a°}]

从原点出发，沿着与x轴逆时针旋转a°的方向，移动一个单位，得到的点的坐标（包括原先的点）。

2、AnglePath[{a°,b°}]

从原点出发，沿着与x轴逆时针旋转a°的方向，移动一个单位，得到第二个点的坐标；

从第二个点出发，沿着与上面那个方向逆时针旋转b°的方向，移动一个单位，得到第3个点的坐标。

3、AnglePath[{{r,a°}}]

从原点出发，沿着与x轴逆时针旋转a°的方向，移动r个单位，得到的点的坐标（包括原先的点）。

4、AnglePath[{{p, 90°}, {q, 90°}, {r, 90°}}]

从原点出发，沿着与x轴逆时针旋转90°的方向，移动p个单位，得到第二个点的坐标；

从第二个点出发，沿着与上面那个方向逆时针旋转90°的方向，移动q个单位，得到第3个点的坐标；

从第三个点出发，沿着与上面那个方向逆时针旋转90°的方向，移动r个单位，得到第4个点的坐标。

5、用线段把“路径”上的点连起来，实现可视化。

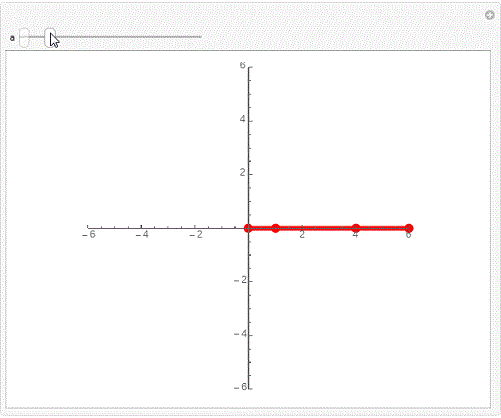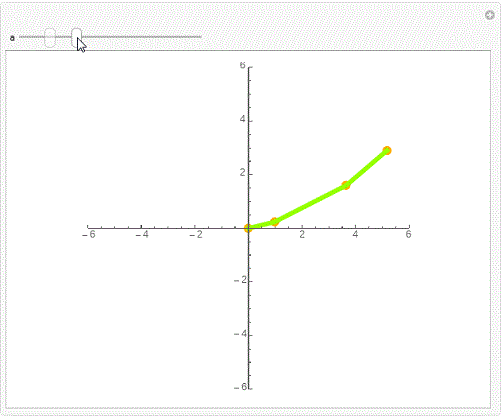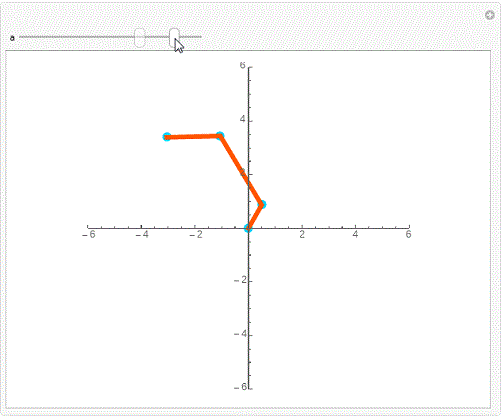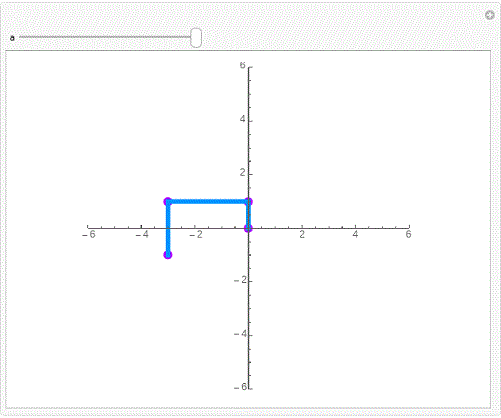
Graphics[Line[AnglePath[{{1, a}, {3, a}, {2, a}}] /.a->60°]],Axes->True]

Graphics[Line[AnglePath[{{1, a}, {3, a}, {2, a}}] /.a->20°]],Axes->True]

Graphics[Line[AnglePath[{{1, a}, {3, a}, {2, a}}] /.a->10°]],Axes->True]

Graphics[Line[AnglePath[{{1, a}, {3, a}, {2, a}}] /.a->120°]],Axes->True]

Graphics[Line[AnglePath[{{1, a}, {3, a}, {2, a}}] /.a->1200°]],Axes->True]

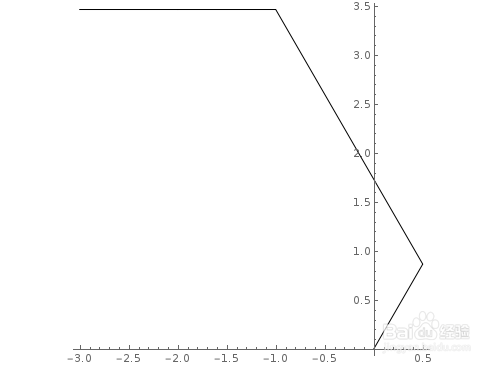
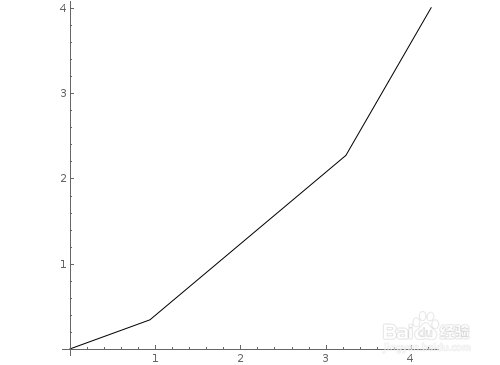
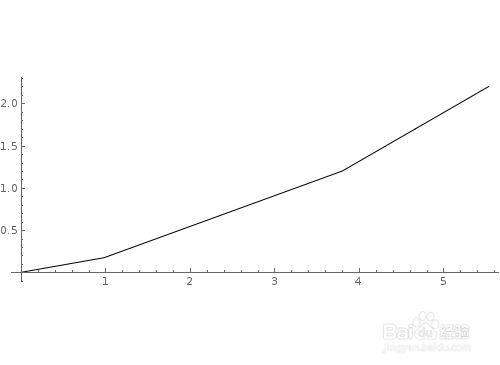
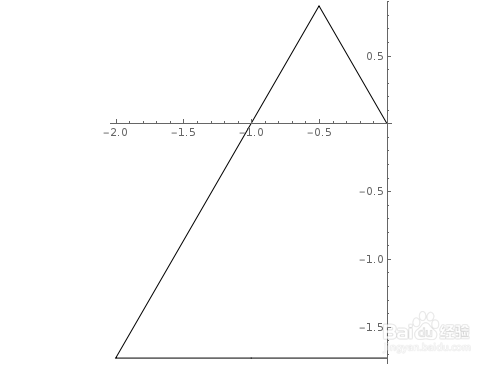
6、再来一个精彩的互动效果。

Manipulate[Graphics[

{Hue[a/2],PointSize[0.02],Point[AnglePath[{{1, a}, {3, a}, {2, a}}]],

Hue[a],Thickness[0.01],Line[AnglePath[{{1, a}, {3, a}, {2, a}}]]},

PlotRange->6,Axes->True],{a,0°,90°}]