用定积分求出四条直线±x±y=1与单位圆围成的面积
1、所围成的面积在第一象限,此步骤是对直线和圆位置关系进行解析。
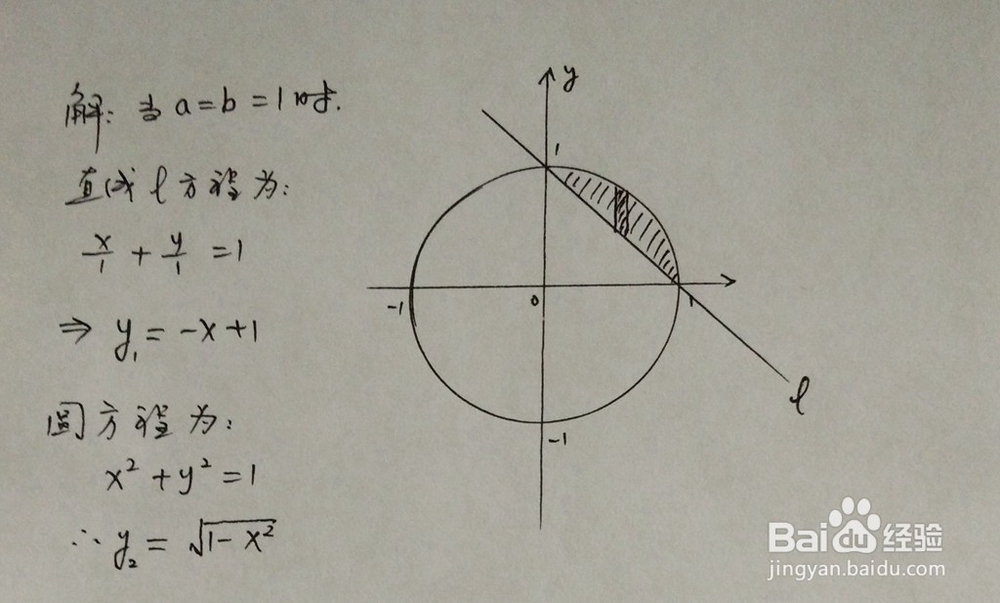
2、定积分计算,以下为计算的主要过程。
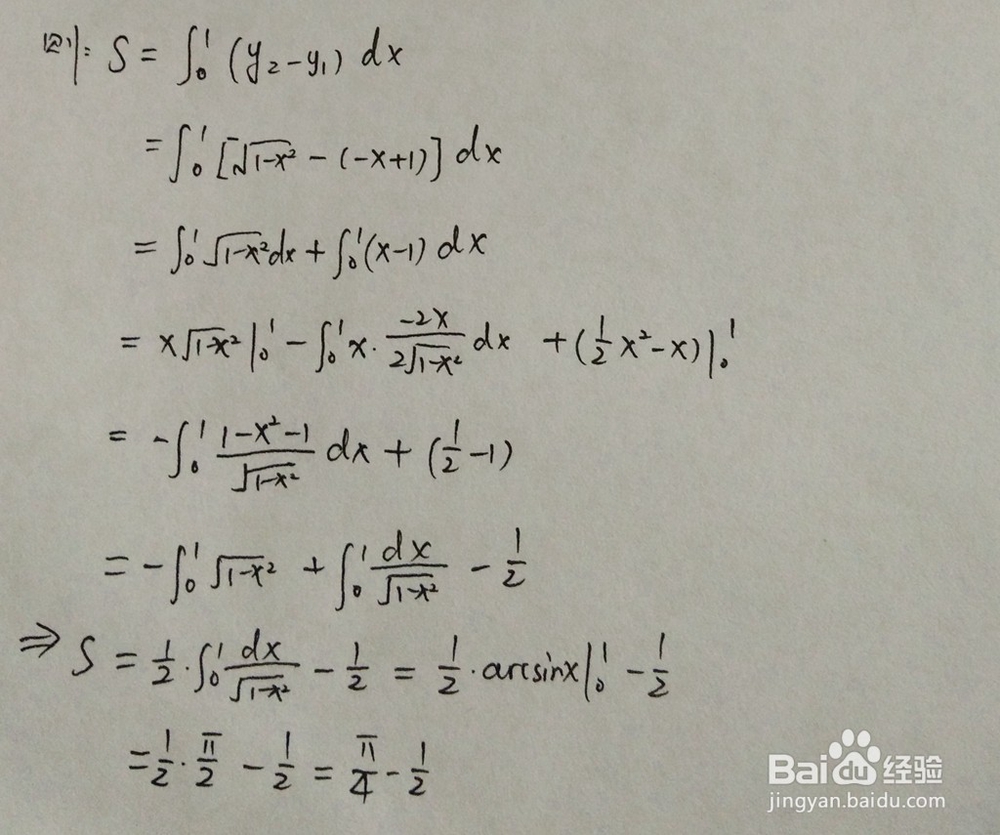
1、所围成的面积在第四象限,此步骤是对直线和圆位置关系进行解析。
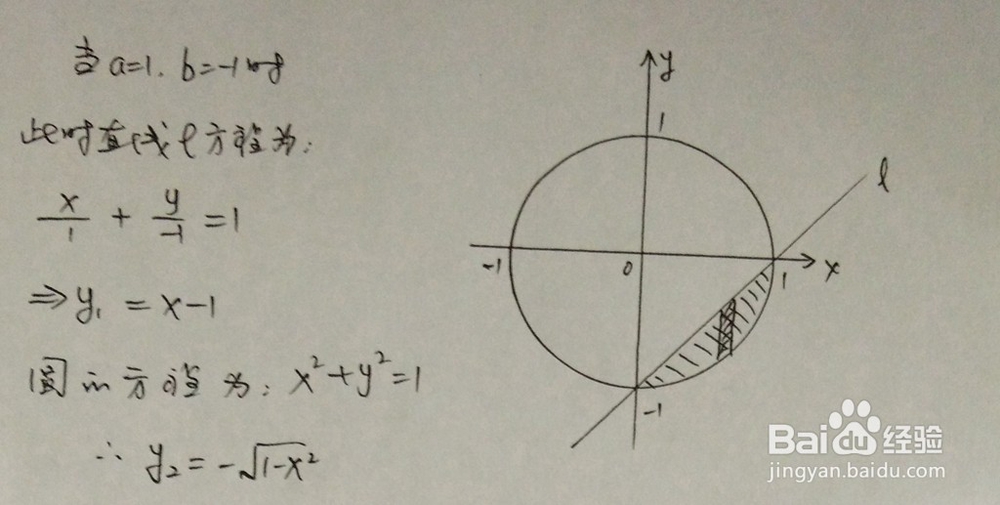
2、定积分计算,以下为计算的主要过程。
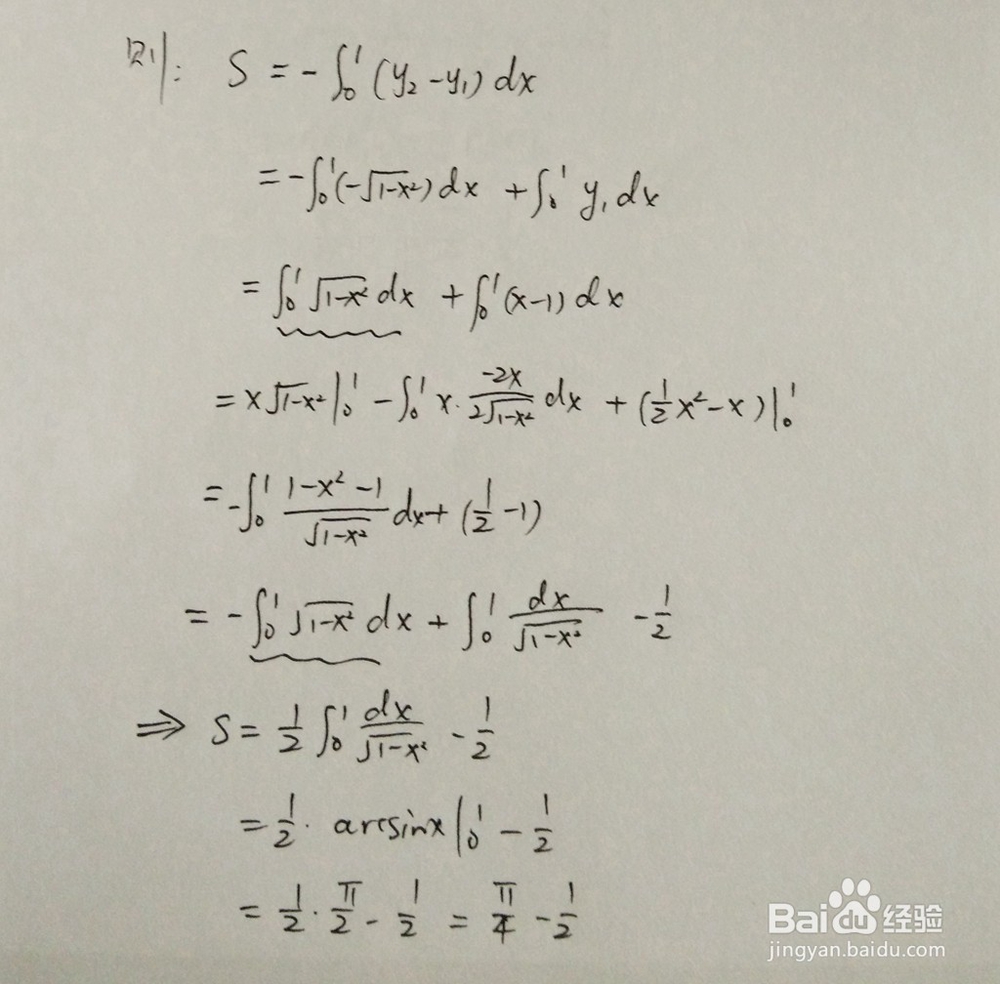
1、所围成的面积在第三象限,此步骤是对直线和圆位置关系进行解析。
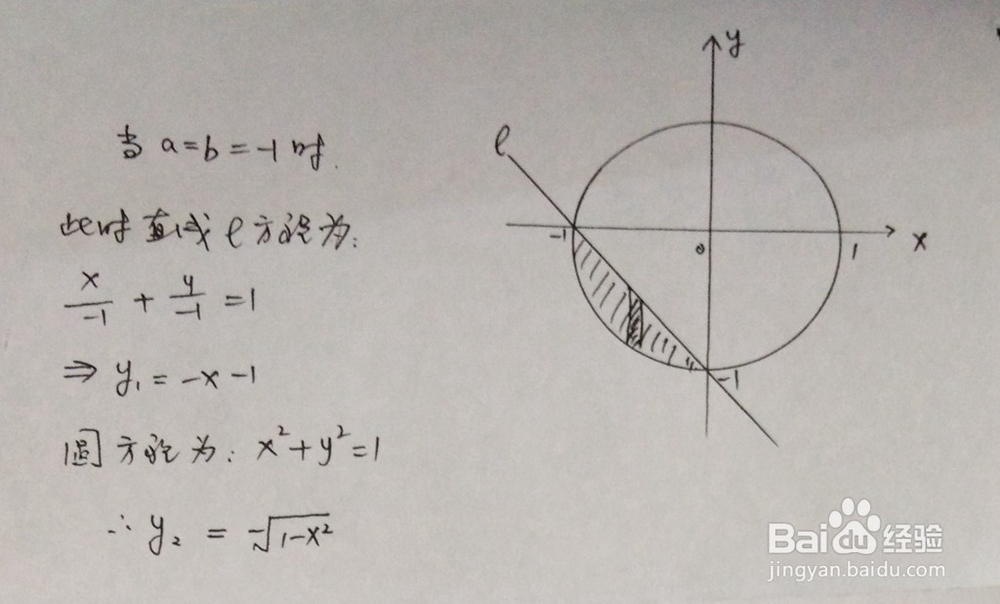
2、定积分计算,以下为计算的主要过程。
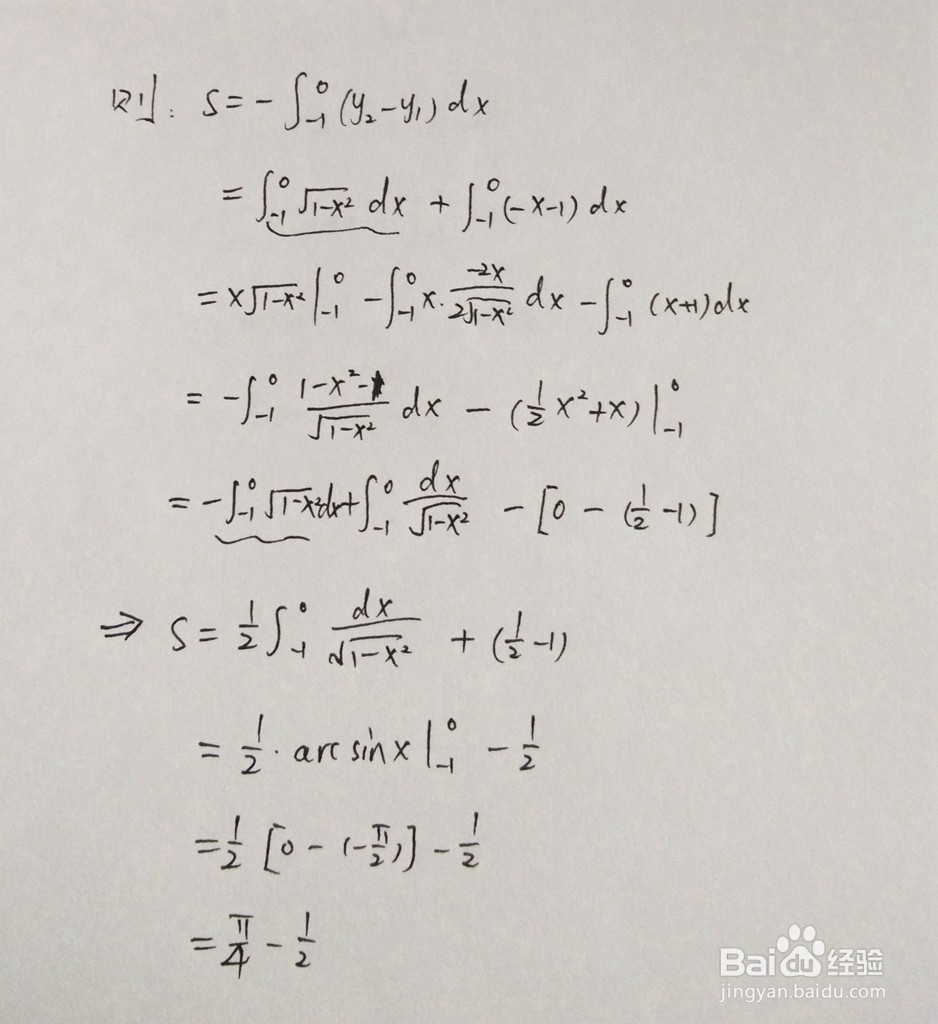
1、所围成的面积在第二象限,此步骤是对直线和圆位置关系进行解析。
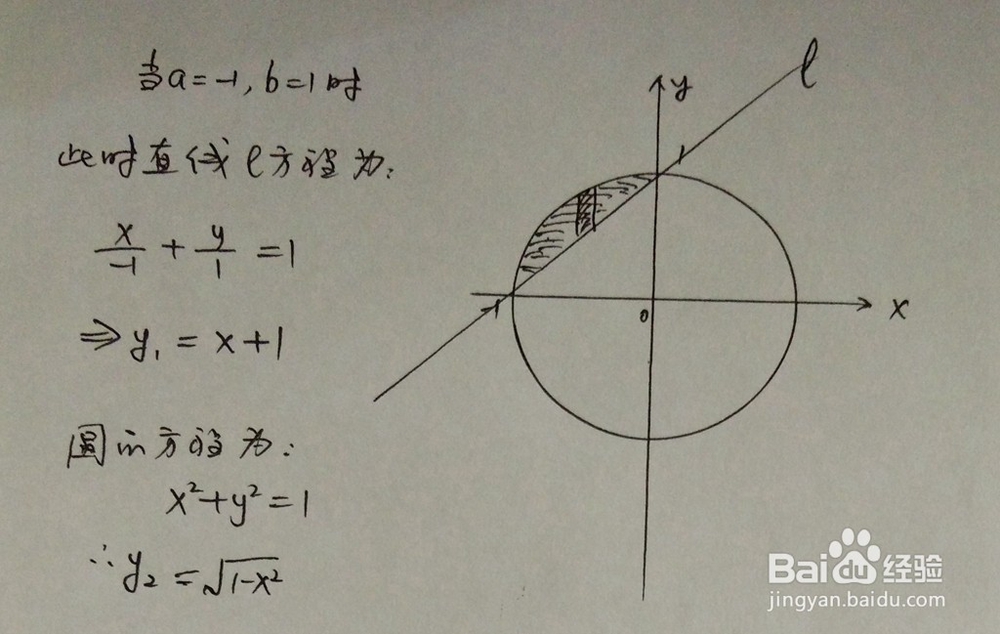
2、定积分计算,以下为计算的主要过程。
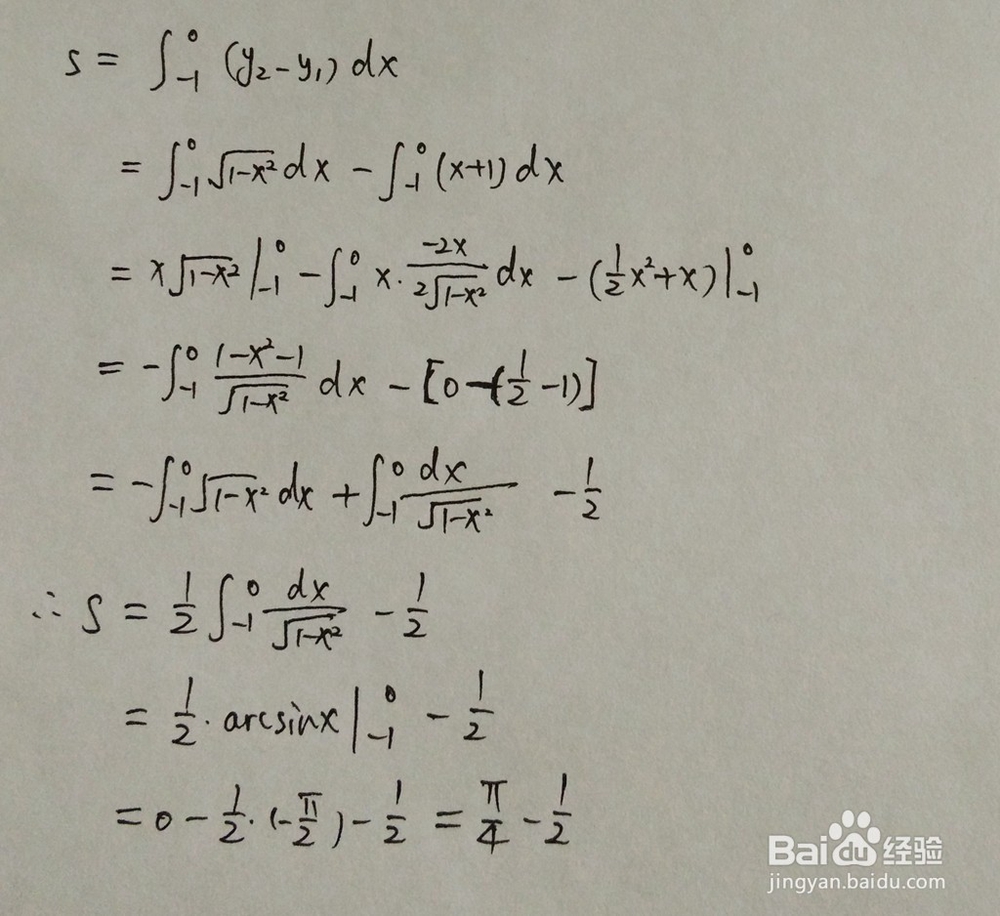
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。