用Mathematica处理几何问题——点、线段

1、        绘制一个点：

Graphics[Point[{2, 3}]]

        注意点的坐标用{}括起来。

2、        绘制多个点：

Graphics[Point[Table[{t, Log[t]}, {t, 0.1, 6, 1/10}]]]

3、        改变点的样式，粉红色的大点：

Graphics[{PointSize[Large], Pink, 

  Point[Table[{Cos[t], Sin[t]}, {t, 0, 2 \[Pi], \[Pi]/10}]]}]

4、        绘制365个随机的点，颜色、大小、位置都是随机的：

Graphics[Table[{Hue[RandomReal[]], PointSize[RandomReal[{0, 0.1}]],    Point[RandomReal[1, {2}]]}, {365}]]

这段代码每次运行，都可能会有不同的结果。

5、        简单地把点分类，用Point画出来：

【{red, green} = 

  Last@Reap@

    Scan[If[#[[1]]^2 + #[[2]]^2 < 2 && #[[1]] + #[[2]] < 1, 

       Sow[#, "Red"], Sow[#, "Green"]] &, 

     RandomReal[{-2, 2}, {8888, 2}]];

Graphics[{{Red, Point[red]}, {Green, Point[green]}}]】

1、        线段，用Line实现。线段的端点的坐标，全放在{英文输入法的括号}里面：

Graphics[Line[{{0, 0}, {3, 4}}]】

2、        画多条线段，围成一个三角形（折线段的端点，这些点的坐标，全放在{英文输入法的括号}里面）。

Graphics[Line[{{0, 0}, {3, 4}, {0, 4}, {0, 0}}]】

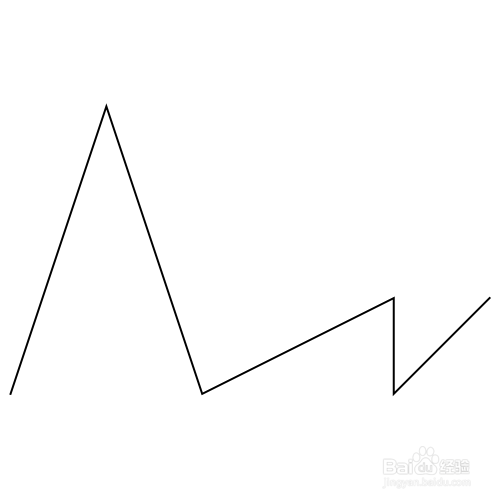
3、        绘制不同样式的线段（注意{}的用法）：

l = Line[{{1, 0}, {2, 3}, {3, 0}, {5, 1}, {5, 0}, {6, 1}}];

Graphics[{Thick, l}, ImageSize -> {500, 500}]】

Graphics[{Thick, Dashed, Blue, l}】

4、        绘制曲线的切向量（这里涉及微分几何的知识）：

With[{f = {Cos[x] + Sin[2 x], 2 Cos[x] + Sin[3 x]}}, 

 Graphics[Table[{Hue[t/(2 Pi), 1, .8], 

     Line[{f, Normalize[D[f, x]] + f}]} /. x -> t, {t, 0, 2 Pi, .05}]】

        和

With[{f = {Cos[3 x] + Sin[2 x], 2 Cos[x] + Sin[3 x]}}, 

 Graphics[Table[{Hue[t/(2 Pi), 1, .8], 

     Line[{f, Normalize[D[f, x]] + f}]} /. x -> t, {t, 0, 2 Pi, .05}]】

5、        绘制有八个点的完全图（这是图论的知识）：

p = Tuples[Table[{Cos[t] + Sin[2 t], Sin[t]}, {t, 0, 2 Pi, 2 Pi/8}],    2];

Graphics[Line[p]】

6、        绘制曲线的切线簇（涉及射影几何、代数几何等理论）：

f[x_] := x^2 + x

p = Table[{{a - 2, f'[a] ((a - 2) - a) + f[a]}, {a + 2, 

     f'[a] ((a + 2) - a) + f[a]}}, {a, -10, 10, .1}];

Graphics[Line[p], PlotRange -> {{-1, 1}, {-1, 1}}】

7、        绘制摩尔的视觉误差条纹：

Graphics[Table[

  Line[{{{x, 0}, {1 - x, 1}}, {{0, x}, {1, 1 - x}}}], {x, 0, 1, .02}]】