参数方程的二阶导数的计算方法

1、先计算y关于x的一阶导数：y'=dy/dx=(dy/dt)/(dx/dt)

2、用Mathematica套公式：yx=D[y,t]/D[x,t]

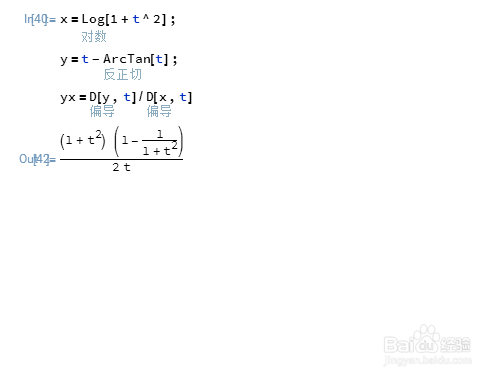
3、化简一下：yx=D[y,t]/D[x,t]//FullSimplify

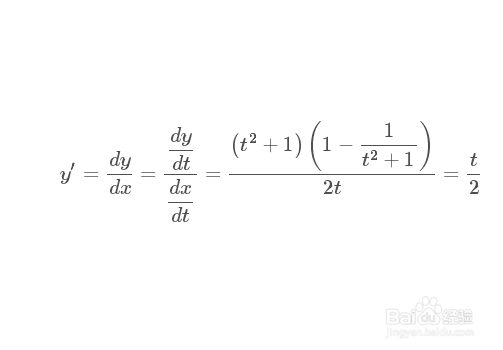
4、二阶导数，其实就是求y的一阶导数关于x的导数：y''=dy'/dx=(dy'/dt)/(dx/dt)

5、在Mathematica里面套公式：yxx=D[yx,t]/D[x,t]这样，我们就得到答案了。

6、而上面的过程，在Mathematica里面，可以整合：x=Log[1+t^2];y=t-ArcTan[t];yxx=D[D[y,t]/D[x,t],t]/D[x,t]//FullSimplify