公务员行测数量关系技巧——排列组合解题技巧

1、一.优先法

例1：2 3 4 5 6 7 8 组成无重复的7位数，数字2必须在首位或末尾，可以有多少种组合方法？

解析：这类问题优先考虑特殊元素，第一步将2可以放在首尾，有两种排法，第二步是剩下的数字全排列，A66=720种，所以总计有1440种情况！

2、二.捆绑法

例2：由ABCDEFG进行排序，ABC三人必须相邻，有多少种排法？

解析：对于有几个特定元素需要单独拿出来考虑的，优先将这几个特定元素捆绑成一个元素来看待，相当于5个元素的全排列，下一步就是ABC内部的排列，有A33种可能性，结果为——A55*A33=720种

3、三.插空法

例3：由ABCDEFG进行排顺序，求ABC必须分开的种类一共有多少?

解析：我们可以先安排剩下的4个人全排列，A44=24，这四个人形成了5个空，安排3个人插入这5个空，有A53种排法，所以根据乘法原理有24*60=1440种排法！

4、四.反向求值法

例4：由1-9组成一个3位数字，有数字重复的情况有多少种?

解析：数字重复无外乎两种情况，3位数重复，就9种情况，2位数重复稍微复杂一点，但我们可以逆向思维，数字重复的组合数=无任何要求的组合数字-无重复的数字的组合数=9*9*9-9*8*7=225种

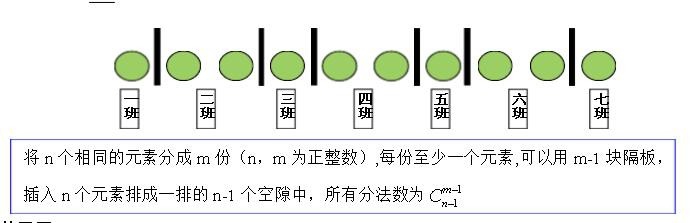
5、五.插板法

例5：10个人，分给7个班级，每个班级至少一个人，多少种分法？

解析：10个人9个空，要分成7份就要插6个板隔开，相当于9个空插6个板，所以有C96=