隐函数2x^(3/2)+5y^(3/2)=3的图像示意图如何？

1、     定义域是指方程习惯中自变量x的取值范围，本题是根据不等式性质来求解自变量x的取值范围。

2、2x^3/2+2y^ 3/2=3

∵2y ^3/2=3-2x^ 3/2≥0，

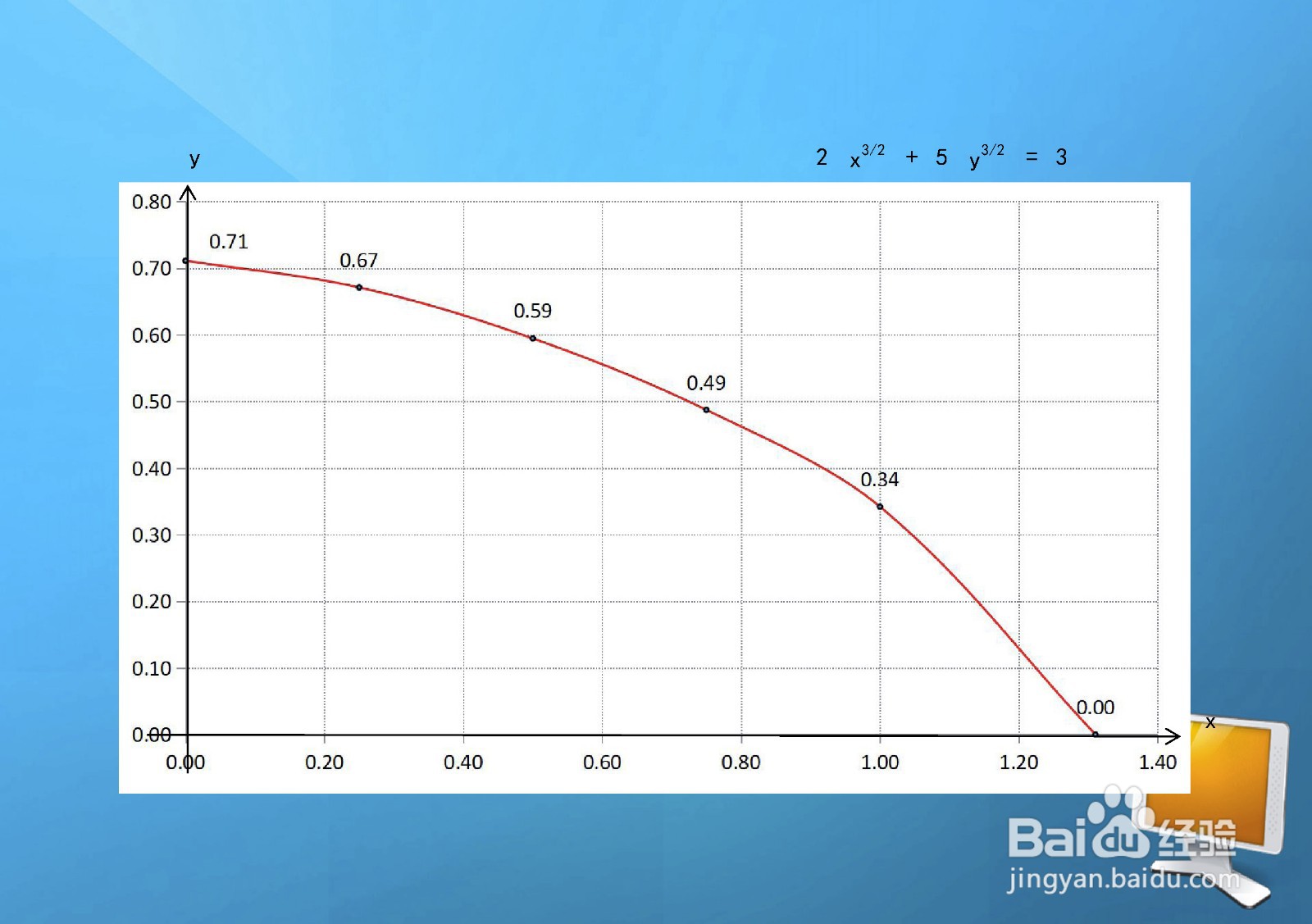
∴x^3/2≤3/2,则：0≤x≤(3/2)^2/3≈1.31.

即函数的定义域为：

[0，1.31 ]

3、判断函数的单调性，主要是求一阶导数，对方程两边同时对x求导，得到导数表达式。

4、2x3/2+5y3/2=3，两边同时求导得：

3x1/2+15/2y'y1/2=0,

y'=-2/5(x/y)1/2

则函数y在定义域上为单调减函数。

5、一阶导数可用于求曲线上某点切线的方程。

例如求曲线上横坐标x=0处点的切线方程。

此时切线的斜率k=y’=0.

则该点处的切线平行于x轴，故切线方程为y=(3/5)^(2/3).

6、对一阶导数y’再次求导，得到二阶导数，可知二阶导数的正负取决于y的正负，当在x轴上方时，y‘’>0,当在x轴下方时，y''<0,进而可以判断曲线方程的凸凹性。

7、∵y'=-2/5(y/x)1/2.

∴y〞=-1/5(x/y)-1/2(y-xy')y-2

=-1/5(y/x)1/2[y+2/5x(x/y)y/x]y

=- 1/25(y/x)1/2(2x3/2+5y3/2)y-5/2

=- 3/25x-1/2y-2

即y〞<0。

则：函数在定义域上为凸函数。

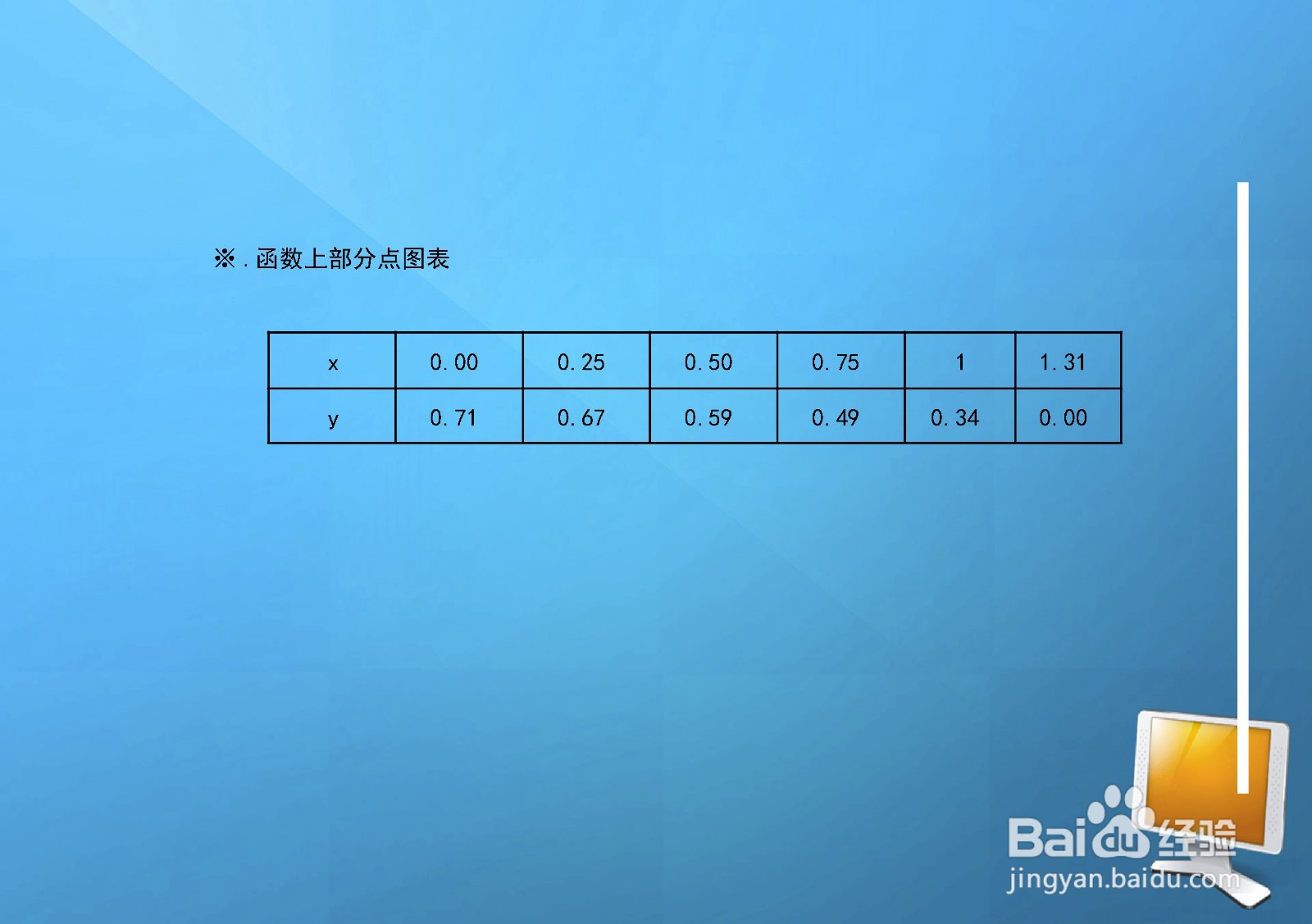
8、曲线方程部分点图表，根据直角坐标系，列举各象限部分点图表如下：

9、根据以上函数的单调性、凸凹性、极限等性质，曲线方程在直角坐标系的示意图如下。