平面上围绕原点旋转的有限群的构造

1、设p[u]是G里面的一个元素：

p[u_] := {{Cos[u], -Sin[u]}, {Sin[u], Cos[u]}}

由于G是有限的，因此必定存在一个正整数n，使得p[u]^n表示恒等变换。

我们先求出p[u]^n：

MatrixPower[p[u], n]

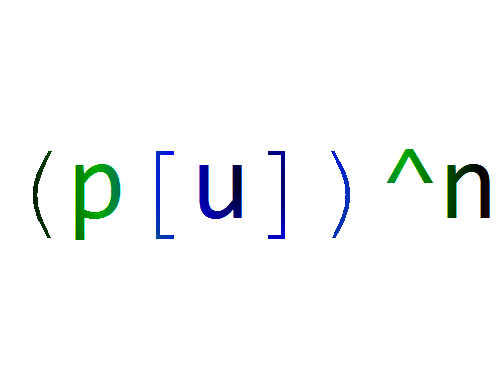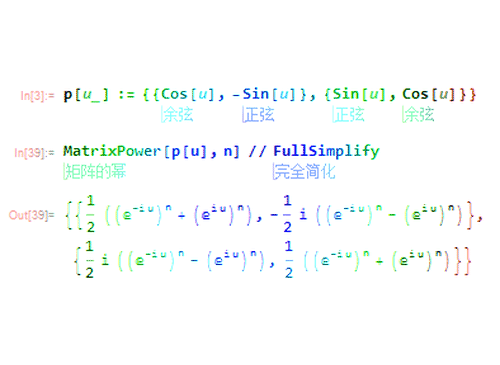
2、不会这么复杂吧！

如果我们限定n的范围，会不会好一些呢？

3、确实可行。

但是，注意，p[u]表示绕原点旋转角度u；

p[u]^n表示，执行n次同样的旋转，其实就是绕原点旋转角度u*n；

所以，p[u]^n=p[u*n]

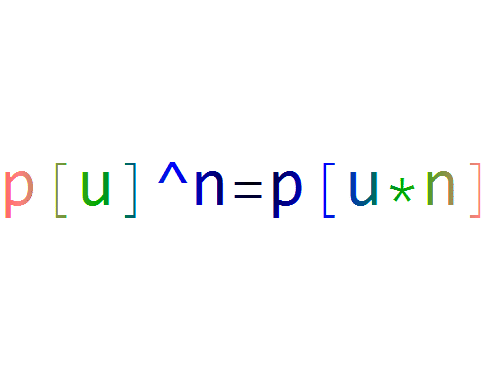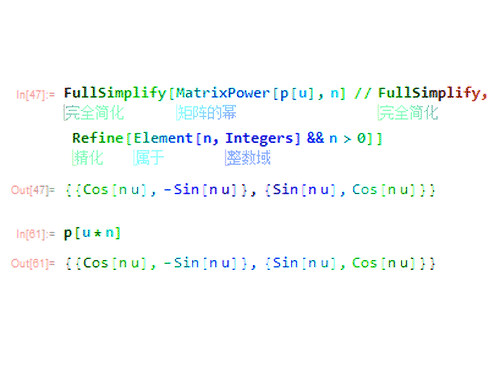
4、假设n是使得p[u*n]为恒等变换的最小的正整数（这样的n肯定是存在的，否则G就是无限群）：

p[u*n] == {{1, 0}, {0, 1}}

可以发现，u=(2cπ)/n，其中c也是整数。

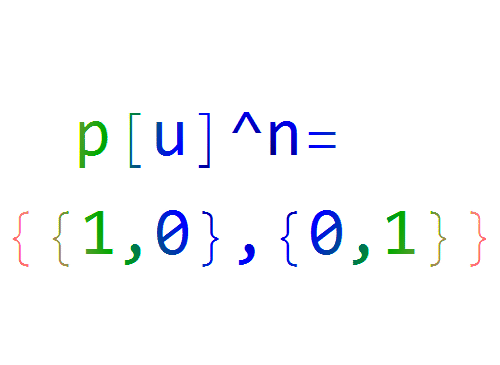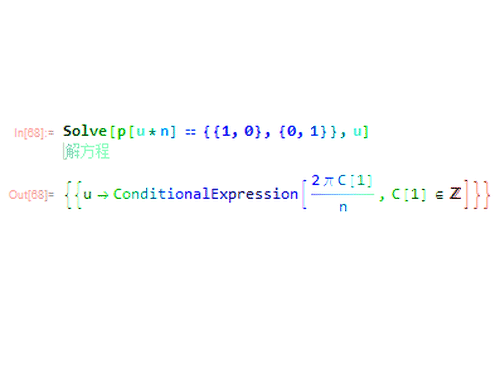
5、这样，集合p[u*r]（r=1,2,3,……,n）

就是G的一个有限子群，记为P；

可以发现，P是有限循环群。

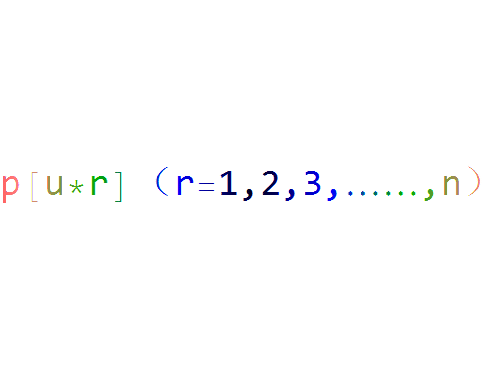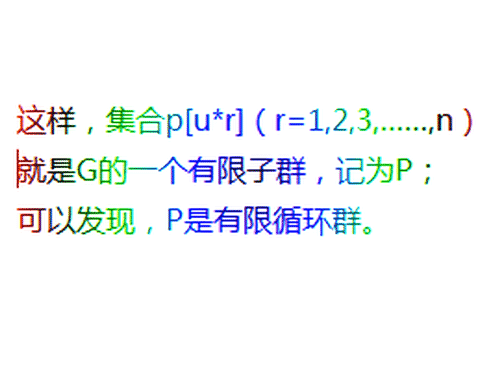
1、假设G-P不是空集，q[v]是G-P里面的元素，表示绕原点旋转角度v：

q[v_] := {{Cos[v], -Sin[v]}, {Sin[v], Cos[v]}}

那么q[v]重复若干次之后，也会回到恒等变换，类似于p[u]；

假设m是最小的正整数，使得：

q[v*m] == {{1, 0}, {0, 1}}

那么，v=(2dπ)/m，其中d也是整数。

q[v*r]（r=1,2,3,……,m）构成G的另一个有限循环子群Q。

2、现在有两个子群了，由于G的封闭性，所以：

p[u]和q[v]的复合，也属于G。

进行这样的操作：

先执行p[u]=p[2π/n]，再执行q[-v]=-q[2π/m]，就相当于绕原点旋转了角度w：

w=2π/n-2π/m

那么，k[w]={{Cos[w], -Sin[w]}, {Sin[w], Cos[w]}}也是G里面的元素，且k[w]不属于P和Q。

3、真正有趣的是，k[w]生成的G的有限循环子群K，会把P和Q囊括在内。

这一点不再多加说明。

4、如果G-K为空集，就说明G为有限循环群。

否则，任取G-K的某个元素，执行上面的操作；

由于G有限，因此，在有限步骤内，就会把G里面的元素全部拿出来。

这就说明，G必定是有限循环群。