证明题不等式—函数思想【高中数学】

在一些不等式证明过旯皱镢涛程中，我们需要灵活的使用学习过的知识点。

解题关键

思维活跃不局限于题干。

敏锐的观察能力。

例题：

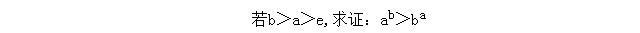
面对这种指数底数都不同的，如何解题一开始我们估计都会比较迷茫。

现在需要仔细分析题目：b＞a＞e这个的作用是什么。为什么要叫你证明大于e,而不是其他的。

第一步：如何利用e

高中阶段用的e的貌似就只有 ①ln x=logex和②lim x→无穷大(1+1/x)^x；

明显利用②会把问题更加复杂化，所以我们应该思考如何利用①。或者说往这方面靠。

ln x这个函数的x>0;且递增！

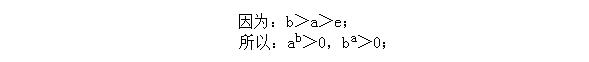
最简单的两边取对数不等式符号不变：

即有：bln a > aln b;现在：

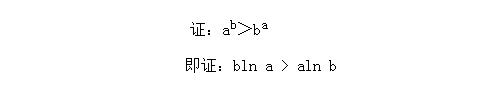
blna>aln b这个式子有如何利用。

还是利用好：b＞a＞e这个关系！

lna/a>lnb/b

证lna/a>lnb/b，巧妙利用函数思想

因为b>a>e;证明lna/a>lnb/b

函数思想比较活跃的看到这一步能反应出就是叫你证明：lnx/x在x>e上递减。

其实你可以把a=x1，b=x2;来让你更容易接近函数思想。或许你看到x才能更好的联系到函数。

要证明：lnx/x在x>e上递减

最简单的是求导思想：(AB)"=AB"+A"B

对ln (x)/x ；x>e;求导得 (1 - lnx)/x²；

因为x>e,(1- lnx)/x²<0;所以：lnx/x在x>e上递减