用Mathematica学习微分几何——空间曲线初步

1、三维空间曲线r[t]的密切平面的方程：

r[t_]:={x[t],y[t],z[t]}

p={x,y,z};

Det[{p-r[t],r'[t],r''[t]}]==0

圆柱螺旋线的密切平面方程是：

r[t_] := {Cos[t], Sin[t], t}

p = {x, y, z};

Det[{p - r[t], r'[t], r''[t]}] == 0

2、空间曲线的逗留点：

如果Cross[r'[t],r''[t]]==0，那么t就是这条曲线的逗留点。

可以证明圆柱螺旋线上面的所有点都不是逗留点：

r[t_] := {Cos[t], Sin[t], t}

Cross[r'[t], r''[t]]

Cross[r'[t], r''[t]].Cross[r'[t], r''[t]]

3、求圆柱螺旋线r[t_]:={Cos[t],Sin[t],t}在点｛1，0，0｝点的密切平面的方程。

稍微计算一下可知，此时t=0，

r[t_] := {Cos[t], Sin[t], t}

p = {x, y, z};

Det[{p - r[t], r'[t], r''[t]}] == 0 // Simplify // TraditionalForm

% /. t -> 0

结果答案很简单，就是平面y==z

4、给出曲线的自然参数方程r[s]，那么它的单位切向量是：

α=D[r[s],s]

曲线的主法向量是：

β=D[r[s],{s,2}]/(D[r[s],{s,2}].D[r[s],{s,2}])

曲线的副法向量为：

γ=Cross[α,β]

以圆柱螺旋线为例，整体代码是：

r[s_] := {Cos[s/Sqrt[2]], Sin[s/Sqrt[2]], s/Sqrt[2]}

\[Alpha] = r'[s] // Simplify

\[Beta] = r''[s]/(Sqrt[r''[s].r''[s]]) // Simplify

\[Gamma] = Cross[\[Alpha], \[Beta]]

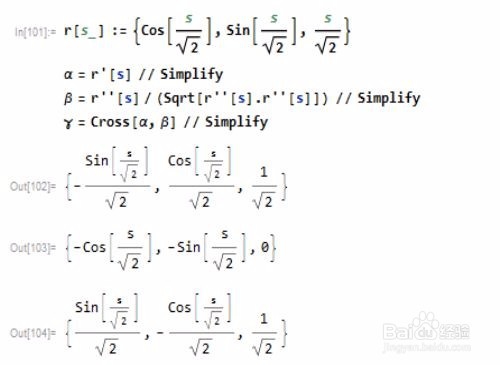
5、自然参数方程条件下，密切平面的方程是：

r[s_]:={x[s],y[s],z[s]}

p={x,y,z};

Det[{p-γ,α,β}]==0

法平面的方程是：

(p-γ).α==0

从切平面的方程是：

(p-γ).β==0

以圆柱螺旋线为例：

r[s_] := {Cos[s/Sqrt[2]], Sin[s/Sqrt[2]], s/Sqrt[2]}

\[Alpha] = r'[s] // Simplify;

\[Beta] = r''[s]/(Sqrt[r''[s].r''[s]]) // Simplify;

\[Gamma] = Cross[\[Alpha], \[Beta]] // Simplify;

p = {x, y, z};

Det[{p - \[Gamma], \[Alpha], \[Beta]}] == 0 // Simplify

(p - \[Gamma]).\[Alpha] == 0 // Simplify

(p - \[Gamma]).\[Beta] == 0 // Simplify

6、对于曲线的一般参数方程r[t]，有 ：

r[t_]:={Cos[t],Sin[t],t}

α=r'[t]/Sqrt[r'[t].r'[t]]//Simplify

β=Cross[r'[t],r''[t]]/Sqrt[Cross[r'[t],r''[t]].Cross[r'[t],r''[t]]]//Simplify

γ=((r'[t].r'[t]) r''[t]-(r'[t].r''[t]) r'[t])/(Sqrt[r'[t].r'[t]] Sqrt[Cross[r'[t],r''[t]].Cross          [r'[t],r''[t]]])//Simplify