怎么用矩阵表示普通的几何变换？

1、我们用ρ[u]来表示几何图形绕原点，逆时针旋转u的操作。

给定点A=(a,b)，旋转之后的点的坐标是：

ρ[u].A={a Cos[u] - b Sin[u], b Cos[u] + a Sin[u]}

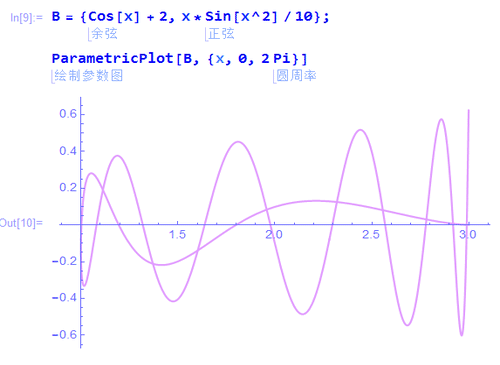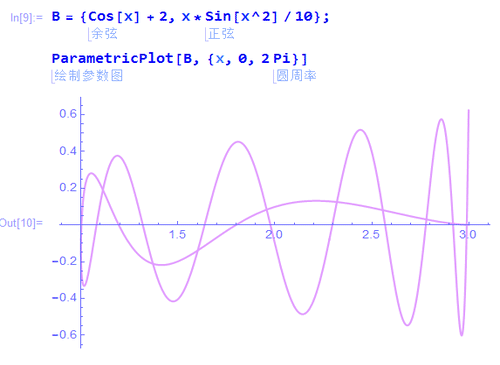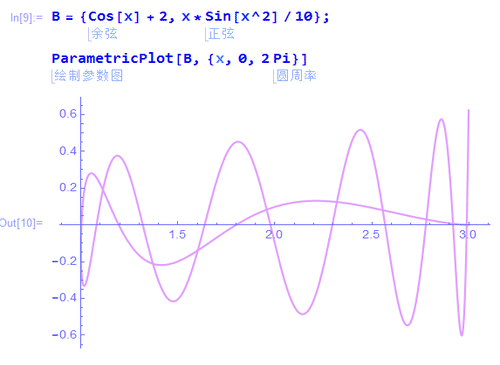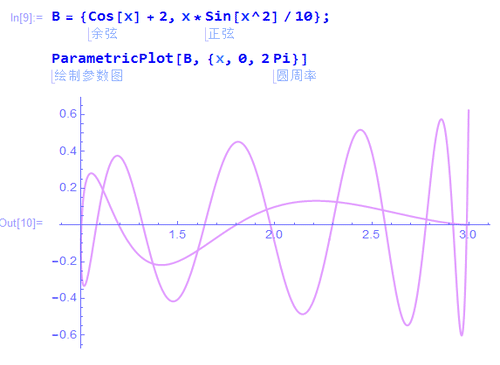
2、给定一条参数曲线B，先绘制其图像：

B = {Cos[x] + 2, x*Sin[x^2]/10}

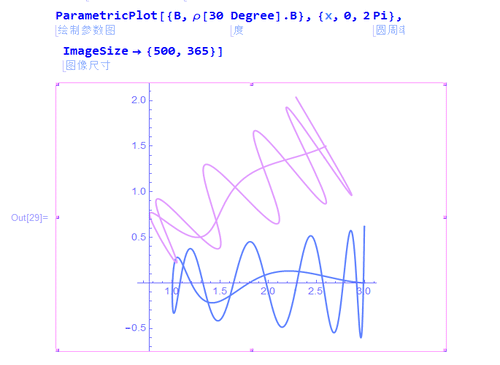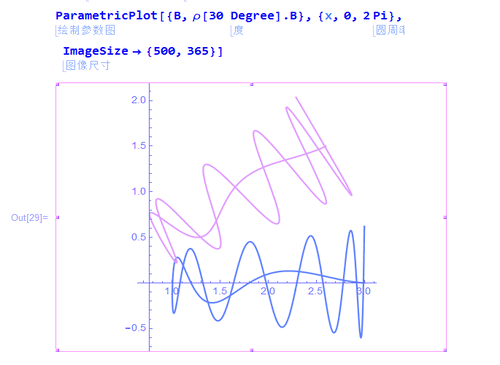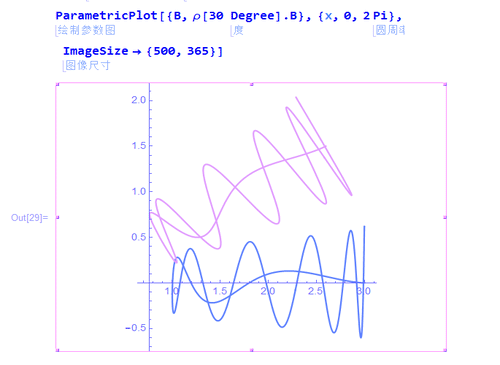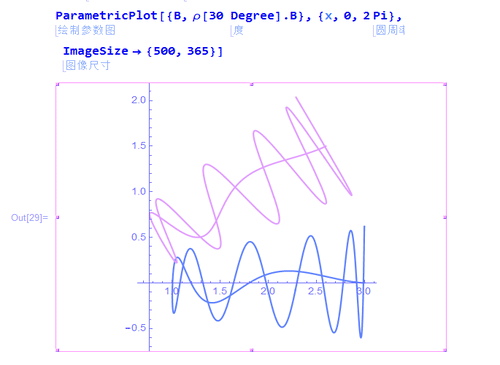
3、看看这条曲线绕原点旋转30°的效果：

ρ[30 Degree].B

4、一系列二维点集，可以构成一个2*n的矩阵，n是点集的点数：

b = Table[

   N[{Cos[x] + 2, x*Sin[x^2]/10}, {2, 2}], {x, 0, 2 Pi, 2 Pi/36}];

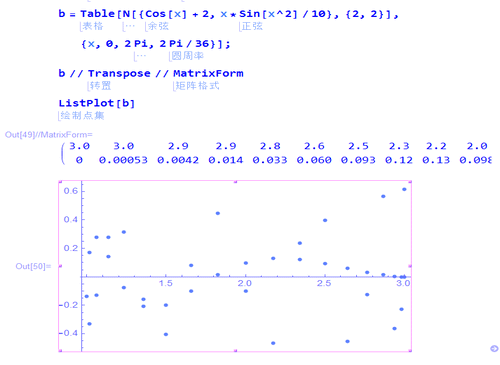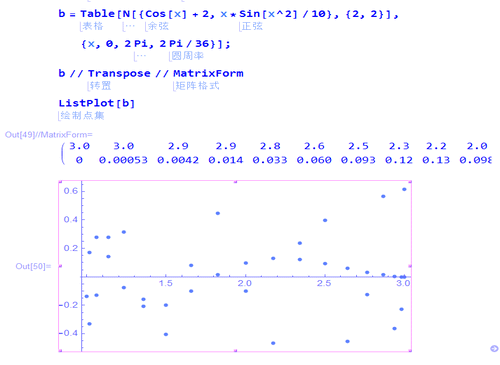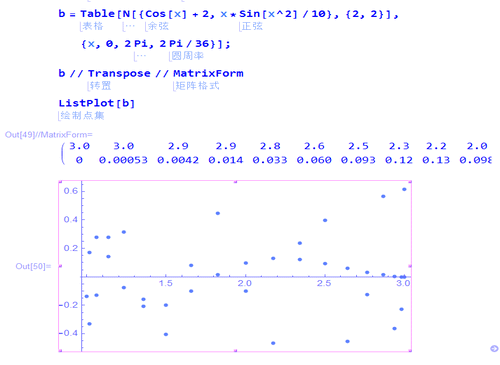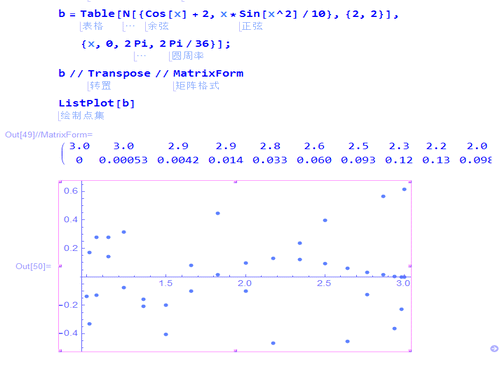
5、用矩阵ρ[36 Degree]，左乘（b//Transpose），可以实现点集旋转36°：

c = (ρ[36 Degree].Transpose[b]) // Transpose

1、平移，其实就更简单了，就是向量的加法运算。比如，把图形B向上平移0.36个单位，就是：

B+{0,0.36}

2、点A（a,b）绕点P（p,q）旋转u，得到的点的坐标，就是：

ρ[u].(A - P) + P

本质是：平移、旋转、平移。