堆排序算法实现

堆排序(Heapsort)是指利用堆积树（堆）烂瘀佐栾这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特盼内溲铫点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。

工具/原料

C/C++

堆的定义

1、n个关键字序列L[n]成为堆，当且仅当该序列满足：1，L(i) <= L(2i)且L(i) <= L(2i+1) 即双亲节点都小于孩子节点2，L(i) >= L(2i)且L(i) >= L(2i+1) 其中i属于[1, n/2]，双亲节点都大于孩子节点。

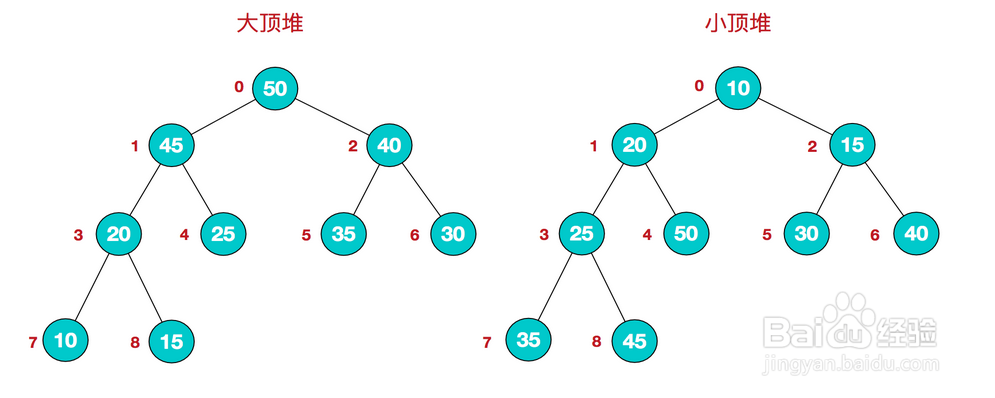
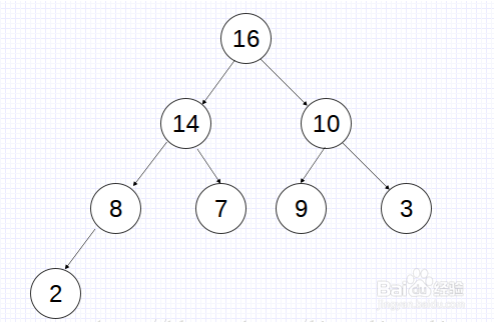
2、满足第一种情况的堆称为小根堆（小顶堆），满足第二种情况的堆称为大根堆（大顶堆）。在大根堆中，最大元素存放在根结点中，且对任一非根结点，它的值小于或等于其双亲结点值。小根堆则恰恰相反，小根堆的根结点存放的是最小元素。例如{16, 14, 10, 8, 7, 9, 3, 2}表示的大根堆：

构造初始堆

1、将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

堆排序

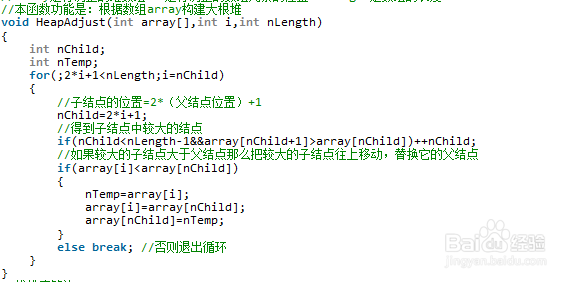
1、构造初始堆成功以后，堆排序的思路就很简单了：首先将存放在L[n]中的n个元素建成初始堆，由于堆本身的特点（以大根堆为例），堆顶元素就是最大值。输出堆顶元素后，通常将堆底元素送入堆顶，此时根结点已不满足大根堆的性质，堆被破坏。这时将堆顶元素向下调整使其继续保持大根堆的性质，再输出堆顶元素。如此重复，直到堆中仅剩下一个元素为止。算法实现如下：构造初始堆成功以后，堆排序的思路就很简单了：首先将存放在L[n]中的n个元素建成初始堆，由于堆本身的特点（以大根堆为例），堆顶元素就是最大值。输出堆顶元素后，通常将堆底元素送入堆顶，此时根结点已不满足大根堆的性质，堆被破坏。这时将堆顶元素向下调整使其继续保持大根堆的性质，再输出堆顶元素。如此重复，直到堆中仅剩下一个元素为止。算法实现如下：

算法性能

1、时间复杂度：向下调整的时间与树高有关，为O(h)。可以证明在元素个数为n的序列上建堆，其时间复杂度为O(n)。之后还有n-1次向下调整操作，每次调整的时间为O(h)，故在最好，最坏和平均情况下，堆排序的时间复杂度为O(nlogn)。

2、空间复杂度：仅使用了常数个辅助单元，空间复杂度为O(1)。