利用MATLAB对Newmark-β法求解振动方程
1、原理如下图公式所示:
其中:Newmark-β正确选择两个参数β和γ很重要;当γ>=1/2, β>=γ/2时,Newmark-β法是无条件稳定的。
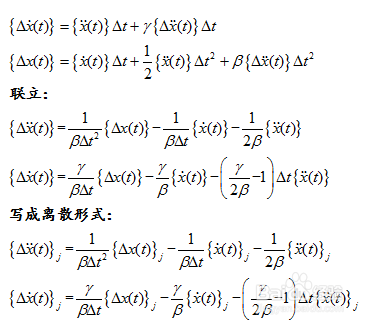
2、代入系统的增量运动方程式,得到Newmark-β法的一系列等效参数,见下图公式所示:

3、算例演示:
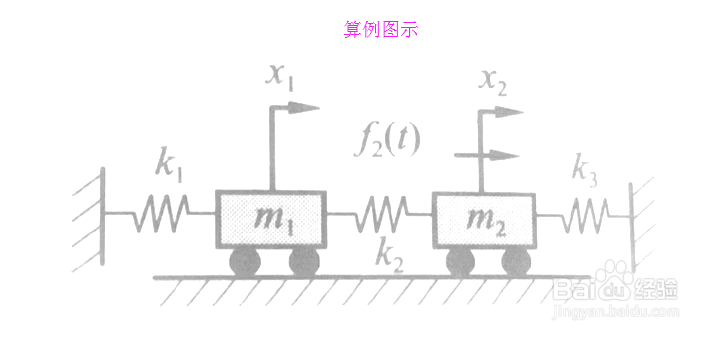
问题:下图所示:一无阻尼两自由度受迫振动系统,已知:m1=1kg、m2=2kg,1=k2=k3=1000N/m,系统在m2上作用有一阶跃激振力f(t)=10N,求解该系统的动力响应。
4、MATLAB程序编写如下:
m=[1,0;0,2]; %% 或m=diag([1,2]),输入质量矩阵
c=[0,0;0,0]; %% 或c=zeros(2),输入质量矩阵
k=[2000,-1000;-1000,2000]; %%输入刚度矩阵
f0=[0;0]; %%输入激励
x0=[0;0]; %%输入初始位移
v0=[0;0]; %%输入初始速度
aa0=inv(m)*[f0-c*v0-k*x0]; %%计算初始加速度
tm=2;dt=0.01;
nt=tm/dt;
x=[x0,zeros(2,nt)];
v=[v0,zeros(2,nt)];
aa=[aa0,zeros(2,nt)];
T=[0:dt:tm];
alfa=0.25;beta=0.5;
a0=1/alfa/dt/dt;
a1=beta/alfa/dt;
a2=1/alfa/dt;
a3=1/2/alfa-1;
a4=beta/alfa-1;
a5=dt/2*(beta/alfa-2);
a6=dt*(1-beta);
a7=dt*beta;
for i=2:nt+1
t=(i-1)*dt;
fi=[0;10];
f=fi;
ke=k+a0*m+a1*c;
fe=f+m*(a0*x(:,i-1)+a2*v(:,i-1)+a3*aa(:,i-1))+c*(a1*x(:,i-1)+a4*v(:,i-1)+a5*aa(:,i-1));
x(:,i)=ke\fe;
aa(:,i)=a0*(x(:,i)-x(:,i-1))-a2*v(:,i-1)-a3*aa(:,i-1);
v(:,i)=v(:,i-1)+a6*aa(:,i-1)+a7*aa(:,i);
end
close all
figure
plot(T,x(1,:)*1000 ,'--b')
ylabel('{\itx}_1/mm')
figure
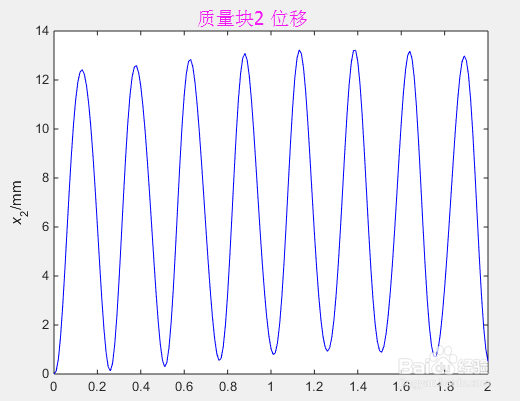
plot(T,x(2,:)*1000,'-b')
ylabel('{\itx}_2/mm')
figure
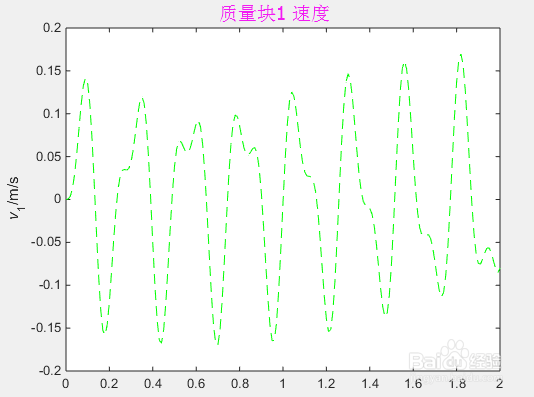
plot(T,v(1,:),'--g')
ylabel('{\itv}_1/m/s')
figure
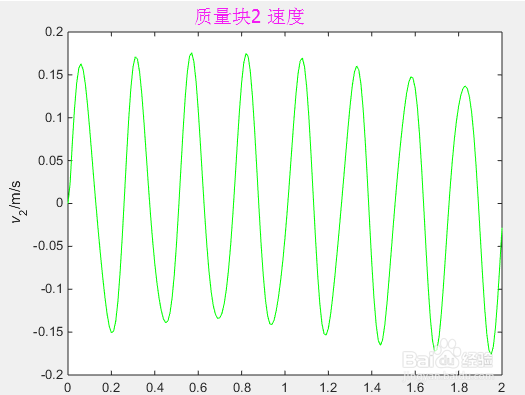
plot(T,v(2,:),'-g')
ylabel('{\itv}_2/m/s')
figure
plot(T,aa(1,:),'--r')
ylabel('{\ita}_1/m^2/s')
figure
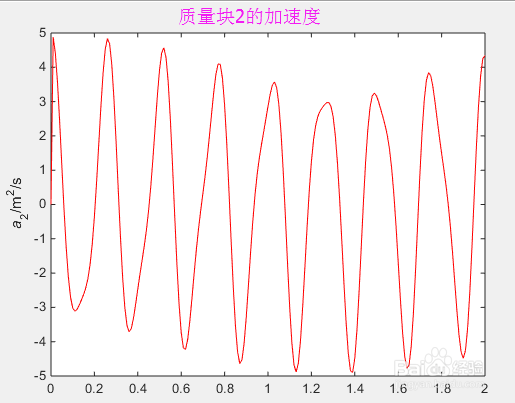
plot(T,aa(2,:),'-r')
ylabel('{\ita}_2/m^2/s'



5、结果显示:在matlab命令窗口输入以上命令,运行上述命令,就可以得到系统的位移、速度、加速度纽马克法数值解,我们用MATLAB画图工具,直观的显示出系统两质量块的位移、速度、加速图时间图,如下图所示: