【微分几何】怎么绘制空间曲线的密切平面？

1、给定曲线的参数方程：

r[t_] := {Cos[3 t], Sin[2 t], t}

aa = ParametricPlot3D[r[u], {u, -Pi, Pi}]

2、我们要绘制曲线上经过点t=π/3的密切平面，先画出这个点的位置：

aa = Show[ParametricPlot3D[r[u], {u, -Pi, Pi}, PlotStyle -> Blue],

  Graphics3D[{PointSize[0.02], Red, Point[r[Pi/3]]}]]

3、密切平面有两个不平行的向量r'[t]和r''[t]确定，我们画出这两个向量：

aa = Show[ParametricPlot3D[r[u], {u, -Pi, Pi}, PlotStyle -> Blue],

  Graphics3D[{PointSize[0.02], Red, Point[r[Pi/3]],

    Green, Arrow[{r[Pi/3], r[Pi/3] + r'[Pi/3]}],

    Orange, Arrow[{r[Pi/3], r[Pi/3] + r''[Pi/3]*0.16}]}]]

4、然后确定密切平面的方程式：

5、绘制密切平面：

aa = Show[ParametricPlot3D[r[u], {u, -Pi, Pi}, PlotStyle -> Blue],

  ParametricPlot3D[{X, Y, Z} /. sol, {X, -Pi, Pi}, {Y, -Pi, Pi}, 

   PlotStyle -> Opacity[0.2], PlotRange -> 1],

  Graphics3D[{PointSize[0.02], Red, Point[r[Pi/3]],

    Green, Arrow[{r[Pi/3], r[Pi/3] + r'[Pi/3]}],

    Orange, Arrow[{r[Pi/3], r[Pi/3] + r''[Pi/3]*0.16}]}]]

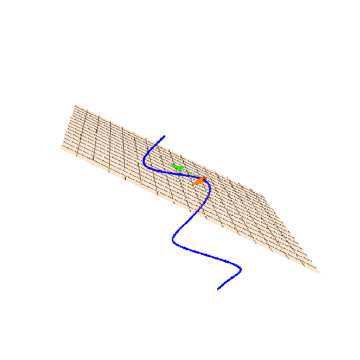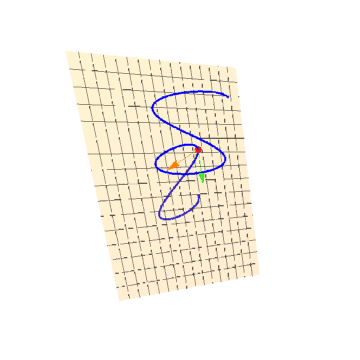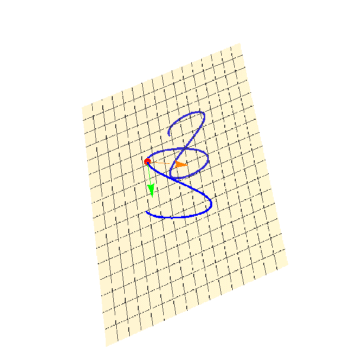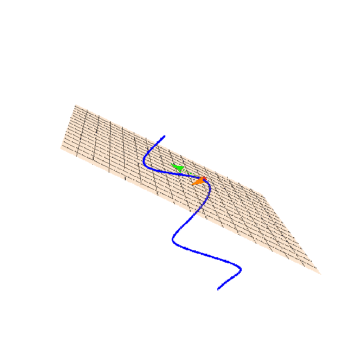
6、一定要注意，上述的两个向量r'[Pi/3]和r''[Pi/3]一定不能平行，否则密切平面就无法确定了。

还有，r'[t]和r''[t]未必是垂直的关系，如下图所示。