椭圆曲线的复变换

1、给定复数z = 5 Cos[t] + 3 I Sin[t]，当t取不同的值，z在复平面上的图形是一个椭圆，椭圆的参数方程，恰好就是复数z的实部和虚部——ReIm[z] :

ParametricPlot[ReIm[z], {t, 0, 2 Pi}, PlotLabel -> z]

2、对z进行平方运算，看看能得到一条什么曲线：

a0 = z^2;

ParametricPlot[{ReIm[z], ReIm[a0]}, {t, 0, 2 Pi}, PlotLabel -> {z, a0}]

注意看，图中的蓝色线就是z对应的椭圆，黄色线就是z^2的图像。

3、如果对z进行开平方呢？

a00 = z^(1/2);

ParametricPlot[{ReIm[z], ReIm[a00]}, {t, 0, 2 Pi}, PlotLabel -> {z, a00}]

4、开平方运算，让图形看起来 "少了一半"。用一个动图来展示一下这个图形的作图过程：

Manipulate[

 ParametricPlot[{ReIm[z], ReIm[an]}, {t, 0, tt}, 

  PlotRange -> {{-5, 5}, {-3, 3}},

  PlotLabel -> {z, an}], {tt, 0.001, 2 Pi}]

5、用动图展示一下z^n，n从0到2之间，图形的变换情况：

Manipulate[

 ParametricPlot[{ReIm[z], ReIm[z^n]}, {t, 0, 2 Pi}, 

  PlotRange -> {{-10, 25}, {-15, 15}}, PlotLabel -> {z, z^n}], {n, 0, 2}]

6、如果对z进行正弦变换，图形如下：

b = Sin[z];

ParametricPlot[{ReIm[z], ReIm[b]}, {t, 0, 2 Pi},PlotLabel -> {z, b}]

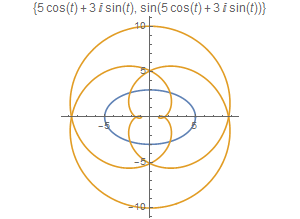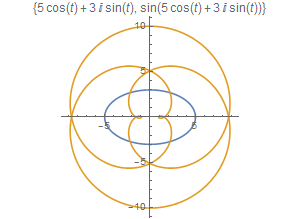
7、Sin[z]的图像的作图过程：

b0 = Sin[z];

Manipulate[

 ParametricPlot[{ReIm[z], ReIm[b0]}, {t, 0, tt}, 

  PlotRange -> {{-9, 9}, {-10, 10}}, PlotLabel -> {z, b0}], {tt, 0.001, 2 Pi}]

8、再来看看Sin[z^n]，n从0到1.2之间变化，对应的图形：

Manipulate[

 ParametricPlot[{ReIm[z], ReIm[Sin[z^n]]}, {t, 0, tt}, 

  PlotRange -> {{-18, 26}, {-24, 24}}, 

  PlotLabel -> {z, Sin[z^n]}], {tt, 0.001, 2 Pi}, {n, 0, 1.2}]