数学分析：函数的几种性质及其判别方法

1、设y=f(x),x∈D

1若存在数M，使f(x)≤M  ,∀x∈D，则称f是有上界的函数

2若存在数L，使f(x)≥L  ,∀x∈D，则称f是有下界的函数

3若存在常数C，使|f(x)|≤C，则称f是有界函数

4若对任意数M，都存在x0∈D，使f(x0)>M ，则称f是无上界函数，同理可定义无下界函数和无界函数

例题如下

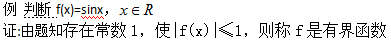
1、设y=f(x),x∈D，∀x1,x2∈D，x1<x2有

1f(x1)≤f(x2)，则称f在D上是递增函数

2f(x1)<f(x2)，则称f在D上是严格递增函数

3f(x1)≥f(x2)，则称f在D上是递减函数

4f(x1)>f(x2)，则称f在D上是严格递减函数

例题如下

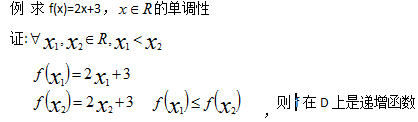
1、设D是对称于原点的数集，y=f(x),x∈D

1若∀x∈D都有f(-x)=f(x)，则称是偶函数

2若∀x∈D都有f(-x)=-f(x)，则称是奇函数

例题如下

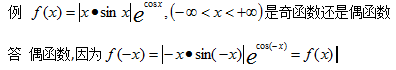
1、设y=f(x),x∈D，若存在正数k，使f(x)=f(x±k)，∀x∈D，则称f(x)为周期函数，k为f的一个周期。若f的所有周期中存在一个最小正周期，则为f的基本周期。

例题如下

1、方法：1定义法

          2画图法

          3看导数正负

例题如下

1、方法：1定义域是否关于原点对称

          2验证f(-x)=f(x)或f(-x)=-f(x)

例题如下

1、方法：1猜周期并加以证明

          2反证法证明不是周期函数

例题如下