使用FWLS处理异方差问题（使用stata）

1、首先我们来看一下FWLS方差处理异方差问题的框架图，在实际问题的处理过程中，我们可以按照此流程进行操作。

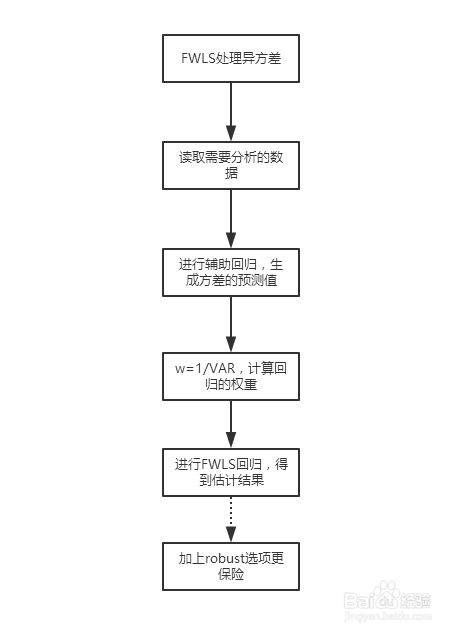
2、先简单介绍一下FWLS方法（更关心如何操作的，可以跳过此步骤）：

F代表的是fesible，也就是可行性。W就是权重，weight。LS代表的则是我们非常熟悉的最小二乘法。观察上条经验中我们提供过的异方差的图片，我们可以发现残差的离散程度会发生变化，也就是残差的方差会变化，也就是存在异方差问题。为什么要加权？因为残差方差较小时，提供的信息量较多（方差小说明残差的波动较小，样本个体之间的差别较小，均值提供的信息也就更多，反之亦然），我们可以取方差的倒数，加大这部分数据在回归方程中的地位，反之，如果方差较大，我们则也取方差的倒数来降低这部分数据在回归方程中的地位。

3、FWLS方法的前置工作（原始回归）

reg y x1 x2 x3

predict e1，r

解释：1.先进性回归，y为被解释变量，x1-x3为被解释变量。

2.predict是预测命令，加上r就是生成残差，e1是变量名，可以更换名称

（图片中的结果，为我根据网络上的数据制作的，你的结果无需和我相同，只要和我格式类似，就说明做对了可以进行下一步操作。）

4、FWLS方法的前置工作（生成变量）

gen e2=e1^2

gen lne2=log(e2)

解释：1.gen命令是生成变量的意思，得出残差的平方项的目的是为了得到方差的估计项。

2.对残差的平方取对数的原因是为了避免后续辅助回归过程中出现方差为负的情况。

（图片中的结果，为我根据网络上的数据制作的，你的结果无需和我相同，只要和我格式类似，就说明做对了可以进行下一步操作。）

5、FWLS方法的前置工作（辅助回归）

reg lne2 x1 x2 x3

解释：残差方差的对数进行辅助回归，看看是不是显著的，把不显著的变量去掉，然后再进行回归。提示：如果常数项不显著只需加上选项，noc即可

predict lne2f

gen e2f=exp(lne2f)

解释：1.先预测残差平方项对数的预测值

2.计算得出残差平方项的估计值。exp（）函数的意思是e^()

完成这些步骤之后即可进行可行性最小二乘法的进一步操作。

下图为辅助回归的结果图（图片中的结果，为我根据网络上的数据制作的，你的结果无需和我相同，只要和我格式类似，就说明做对了可以进行下一步操作。）

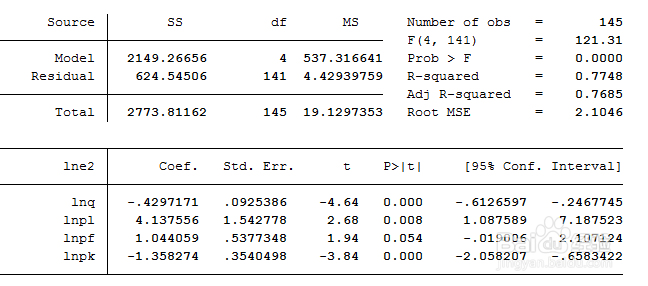
6、FGLS模型回归

reg y x1 x2 x3 [aweight=1/w]

解释：w为权重你只需要把你对应的权重变量填入就可以了，也就是我们在上一步中生成的最后一个变量e2f。（图片中的结果，为我根据网络上的数据制作的，你的结果无需和我相同，只要和我格式类似，就说明做对了可以进行下一步操作。）