怎么用正三角形切割出一个最大的圆？

1、首先，画出点A和点O，这两个点是自由点。

2、构造变量a，最小值为3；

计算：

m5=2*a；

m6=360/a。

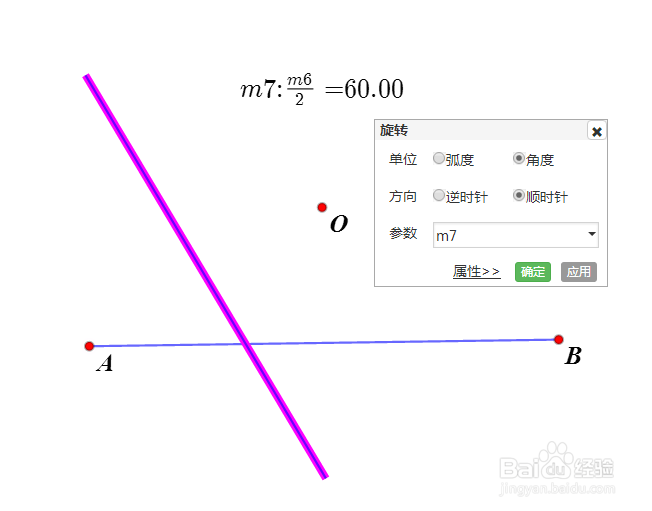
3、点A绕点B逆时针旋转m6的角度，得到点B，连接线段AB。

m6是上一步计算的结果。

4、计算：m7=m6/2；

线段AB绕O顺时针旋转m7的角度，得到另一条线段；

设这条线短与AB交于点I。

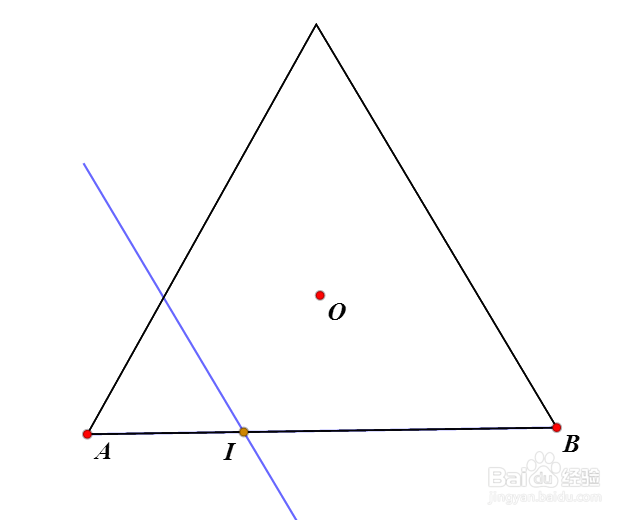
5、以AB为边，构造正m5边形，要求这个正三角形与O位于AB同侧。

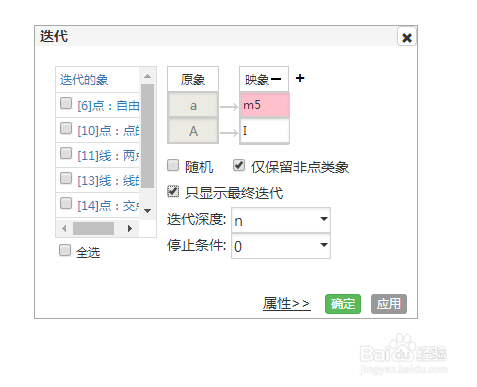
6、迭代规则：

a→m5，

A→I，

只保留非点类像，只保留最终迭代，

迭代深度为n。

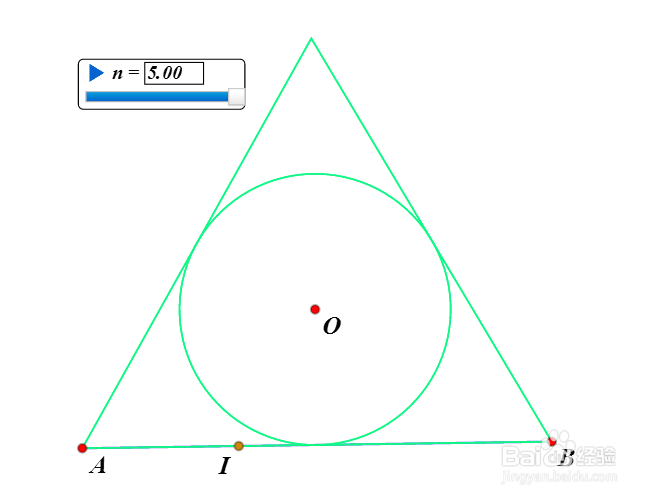
7、构造变量n，最小值为1，最大值为5。

当n=1，2，3的时候，图形如下。

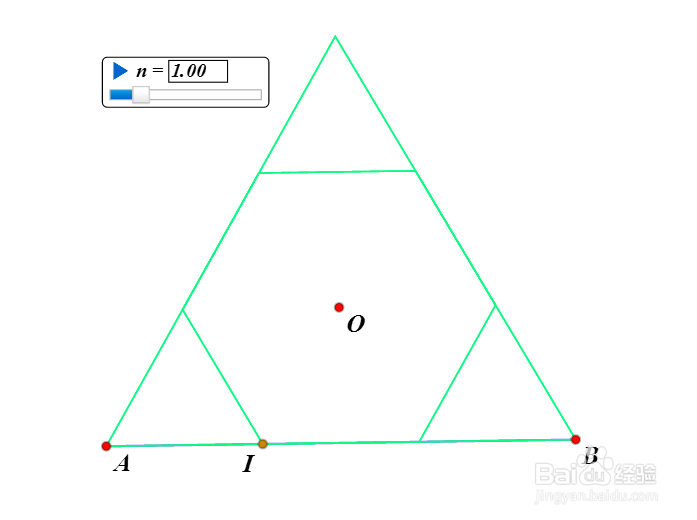
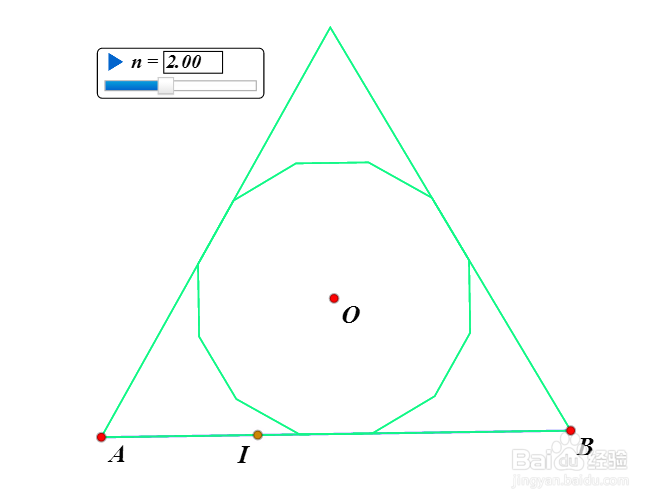
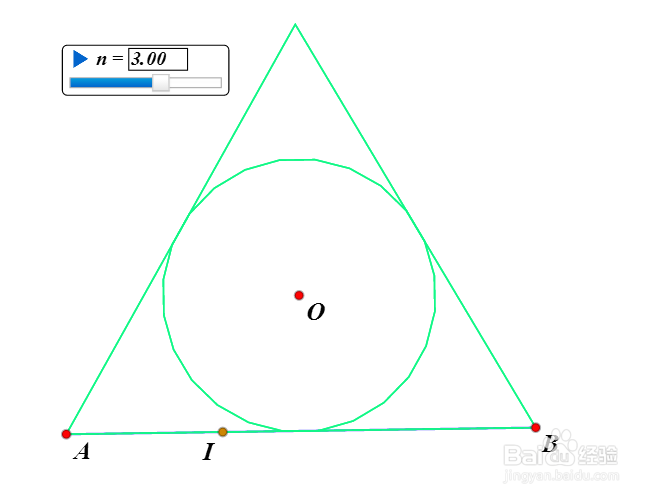
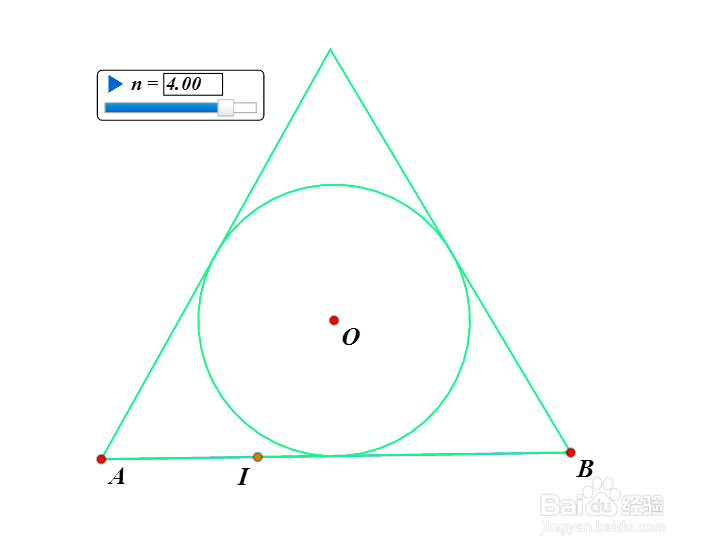
8、当n=4，5的时候，图形已经很难和圆区分开来了。