怎么求函数的分数阶导数？兼谈数学手册计算器

1、尝试着用Mathematica来计算正弦函数的1/2阶导数，无果。

I try to use Mathematica to calculate the 1/2 order derivative of sine function, but no result.

D[Sin[x],{x,1/2}]

2、但是，数学手册却可以办到。

But the MathHandBook can do.

先输入sin(x)，然后点击“半阶导数”按钮，就可以看到结果。

Click sin(x), then click the “semi derivative” button to get result .

3、所以，这里暂时忽略Mathematica。

计算sin(x)的1/3阶导数，就没有固定的按钮可以使用了，需要自己写代码，然后按回车。

So, Mathematica is ignored here for the moment.

Solve the 1/3 order derivative of sin(x), there is no fixed button can be used, You need to write your own code, and then press enter.The code reads as below:

d(sin(x),x,1/3)

4、如果要考虑较一般的情形，可以尝试用下面这段代码：

If You want to find a general case, You can try  the following code:

d(sin(x),x,1/n)

5、不过上面代码的运行结果有点问题，实际上是下图所示。

However, the run-result of the above code has a minor mistake and is actually shown in the following figure.

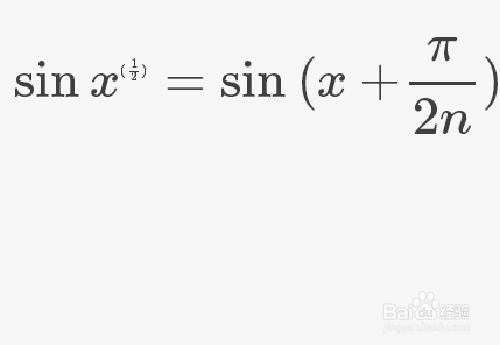
6、更一般的情形。

More general situation:

d(sin(x),x,m/n)

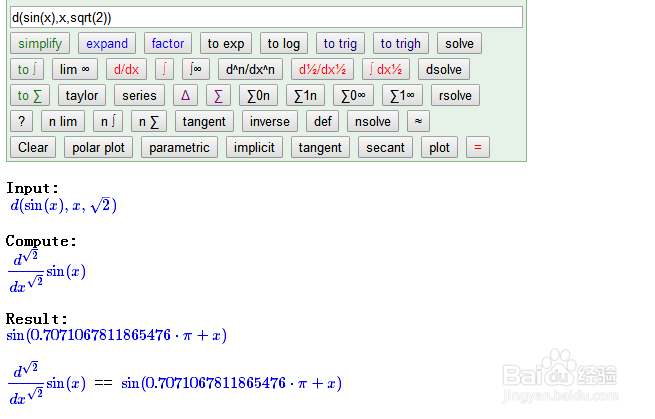
7、能不能求出无理数阶导数呢？比如计算正弦函数的sqrt(2)阶导数。

Can it get the irrational number order derivative? 

For example, the sqrt(2) order derivative of the sine function .

d(sin(x),x,sqrt(2))

运行结果采用了浮点数表示的：

The results are represented by floating-point numbers:

sin(0.7071067811865476*pi+x)

而这个常数0.7071067811865476恰好就是sqrt(2)/2的前16位小数形式。

And this constant 0.7071067811865476 happens to be the first 16 Decimal forms of sqrt (2) /2.

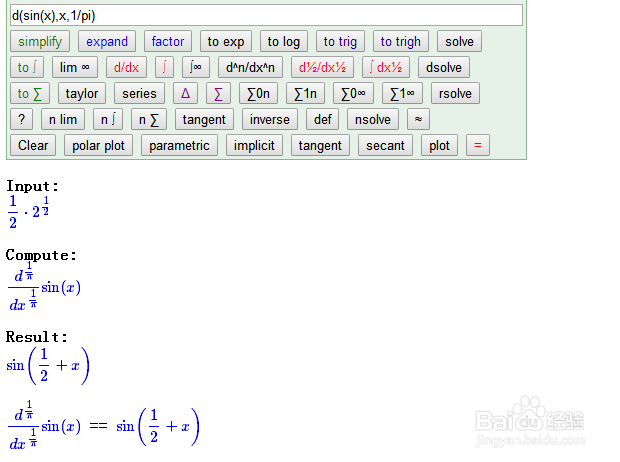
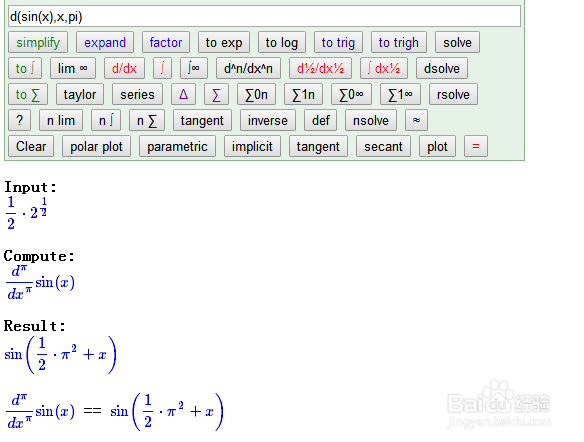
8、正弦函数的π阶导数和1/π阶导数。

The π order derivative and the 1/π order derivative of sine function.

d(sin(x),x,pi)

d(sin(x),x,1/pi)