平移变换，能用矩阵乘法实现吗

1、首先，给定向量箪滹埘麽v={1,2}，作为平移向量。那么，平移就可以用向量加法表示：v = {1, 2};A = {a, b};A + v

2、假设存在一个矩阵P，使得P.A实现了A按照v的平移：P={{p,x},{y,q}}其中，x和y是待定的未知数。

3、如果想要矩阵乘法实现平移，就需要对向量钽吟篑瑜A，P.A=A+v成立。解方程：Solve[P.A == A + v, {x, y}]就可以求出x和y的值来，进而确定P。

4、这时候，矩阵P左乘A，确实实现了A按照v的平移：P.A == A + v这不是多此一说吗？

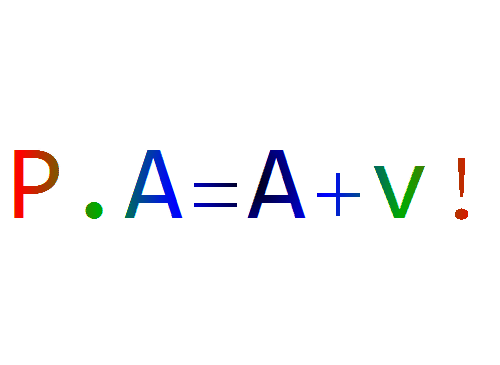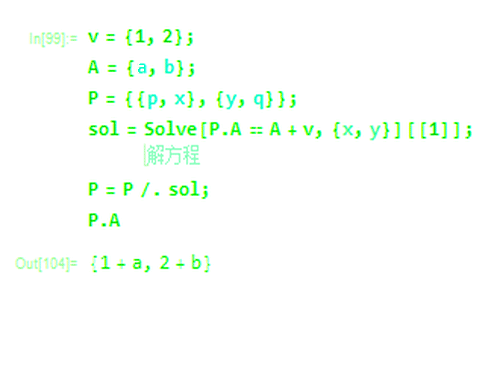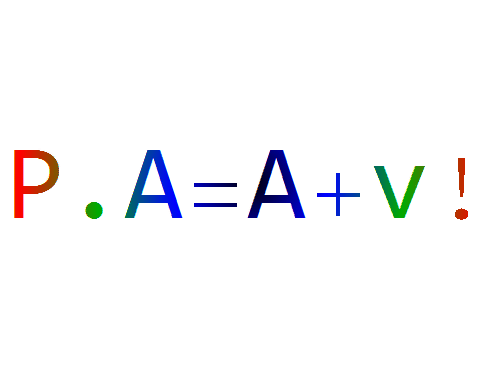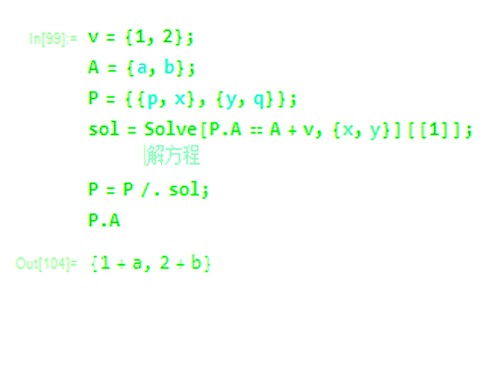
5、但是，当P左乘-A的时候，你就会发现，-A按照-v平移，才会得到P.(-A)的结果。

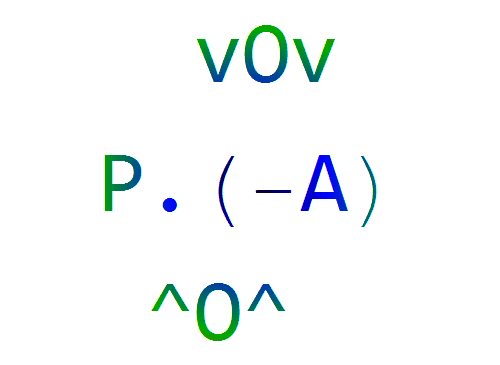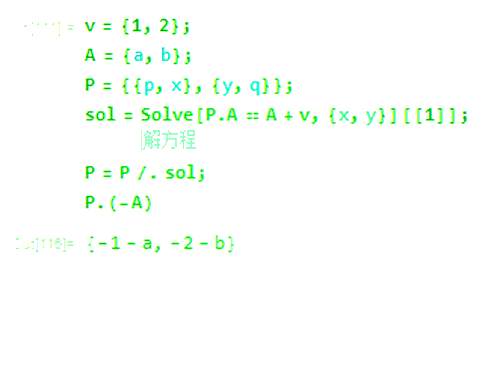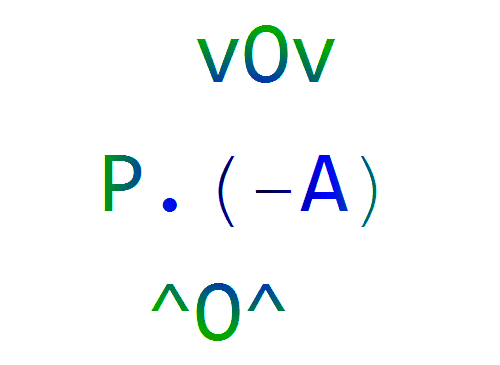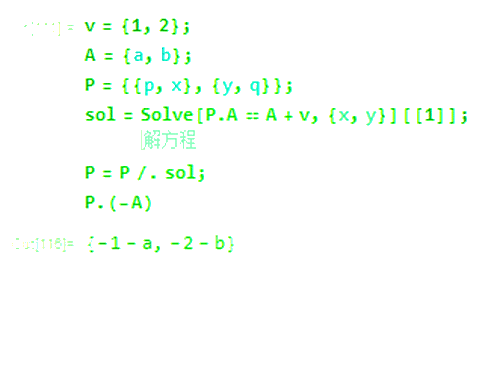
6、实际上，P只对那特定的A才有意义。如果P.M - M == v，那么M只能等于A。

7、这说明，矩阵左乘，不可能是整个平面空间的平移变换。从线性变换的角度看，平移因为没有不动点，所以不存在变换矩阵。