MATLAB利用BP神经网络计算异或(XOR)问题
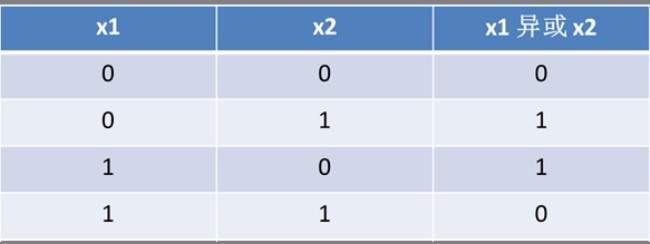
1、首先列出了异或逻辑的基本规则:
0 xor 0=0
0 xor 1=1
1 xor 0=1
1 xor 1=0
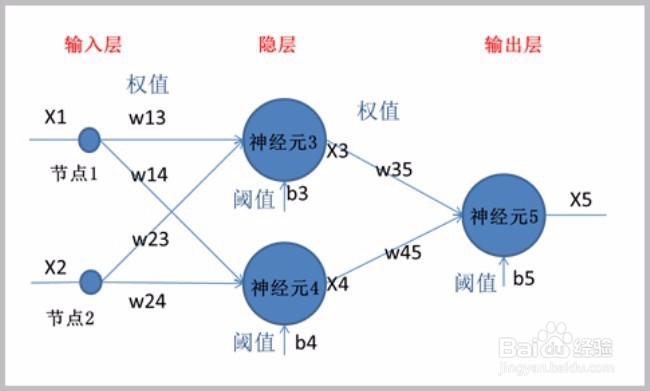
2、我们设计了如下图所示的神经网络,包含3个神经元,3层网络。隐层含有2个神经元,输出层有一个神经元。该神经网络具有两个输入一个输出。
3、【正向传递】在Bp算法中,正向信号传递,反相误差修正。
在每个神经元中,输入与输出的关系如下图所示。
wij表示神经元i与神经元j之间的权值,xi表示神经元i的输出,xj表示神经元j的输出,bj 表示神经元j的阈值。
激活函数函数f(x)在本经验选择S型函数

4、【反向误差修正】首先是隐层与输出层之间误差修正的原理。如下图所示。j表示输出层的神经元,i表示与输出层连接隐层的神经元。wij为神经元i与神经元j之间的权值。
在BP神经网络中,误差信号反向传递子过程比较复杂,它是基于Widrow-Hoff学习规则的。Widrow-Hoff学习规则 是通过沿着相对误差平方和的最速下降方向,连续调整网络的权值和阀值

5、【反向误差修正】其次是输入层与隐层之间的权值阈值调整过程。k为输入层的节点,i为隐层的节点。wki为节点k与神经元j之间的权值

6、下图是本经验所构建的神经网络的权值与阈值修正公式。每层只举一个例子。

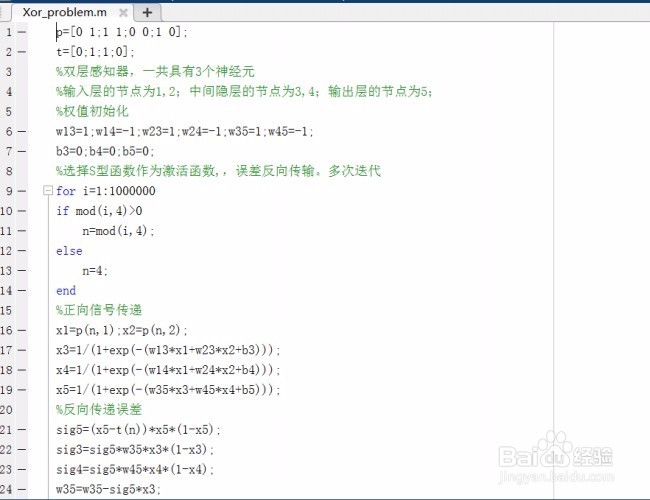
7、Matlab代码如下:
p=[0 1;1 1;0 0;1 0];
t=[0;1;1;0];
%双层感知器,一共具有3个神经元
%输入层的节点为1,2;中间隐层的节点为3,4;输出层的节点为5;
%权值初始化
w13=1;w14=-1;w23=1;w24=-1;w35=1;w45=-1;
b3=0;b4=0;b5=0;
%选择S型函数作为激活函数,,误差反向传输。多次迭代
for i=1:1000000
if mod(i,4)>0
n=mod(i,4);
else
n=4;
end
%正向信号传递
x1=p(n,1);x2=p(n,2);
x3=1/(1+exp(-(w13*x1+w23*x2+b3)));
x4=1/(1+exp(-(w14*x1+w24*x2+b4)));
x5=1/(1+exp(-(w35*x3+w45*x4+b5)));
%反向传递误差
sig5=(x5-t(n))*x5*(1-x5);
sig3=sig5*w35*x3*(1-x3);
sig4=sig5*w45*x4*(1-x4);
w35=w35-sig5*x3;
w45=w45-sig5*x4;
b5=b5-sig5;
w13=w13-sig3*x1;
w23=w23-sig3*x2;
w14=w14-sig4*x1;
w24=w24-sig4*x2;
b3=b3-sig3;
b4=b4-sig4;
end
%输出
for i=1:4
x1=p(i,1);x2=p(i,2);
x3=1/(1+exp(-(w13*x1+w23*x2+b3)));
x4=1/(1+exp(-(w14*x1+w24*x2+b4)));
x5=1/(1+exp(-(w35*x3+w45*x4+b5)))
end
x=p(:,1);y=p(:,2);
plot(x,y,'o');hold on;
x=-0.5:0.1:1.5;
y=-w13/w23*x-b3/w23;
plot(x,y);hold on;
x=-0.5:0.1:1.5;
y=-w14/w24*x-b4/w24;
plot(x,y);hold on;

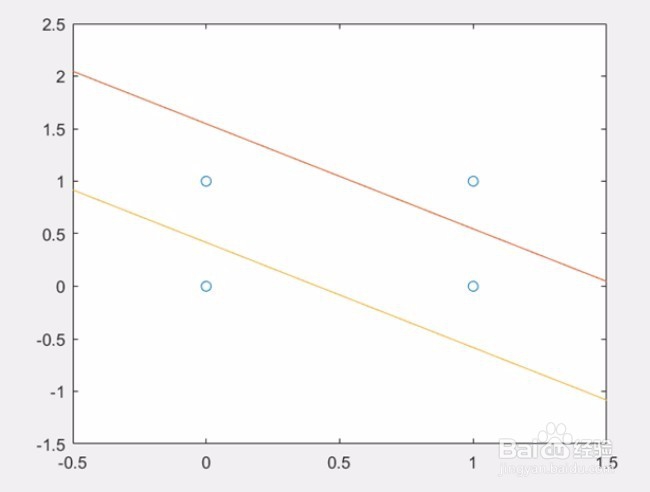
8、可以发现训练迭代的次数越多,更能取得与真实值更接近的结果。隐层两神经元可将四个数据划分成三个区域,解决了Xor问题线性不可分的问题