三角形旁心的概念及一些结论

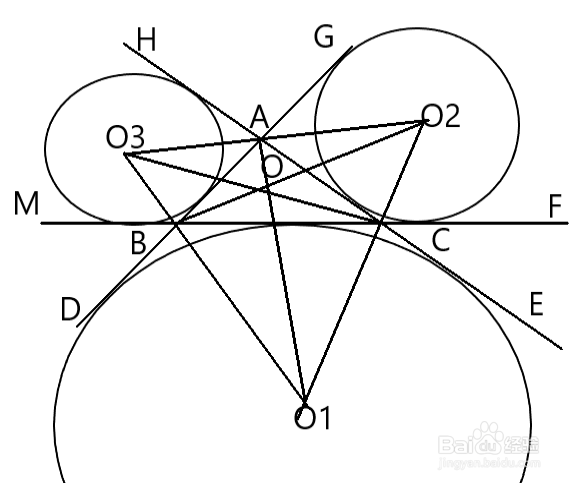
1、三角形旁切圆的圆心,简称为三角形旁心，它是三角形一个内角的平分线和其他两个内角的外角平分线的交点；任何三角形都存在三个旁切圆，三个旁心，旁心都在三角形外部。如图，在△ABC中，∠BAC、∠DBC和∠ECB的角平分线交于点O1，∠ABC、∠FCA、∠GAC的角平分线交于点O2，∠ACB、∠HAB和∠MBA的角平分线交于点O3，点O1、O2、O3就是△ABC的旁心。其中，AO1、BO2、CO3交于点O，点O就是△ABC的内心。

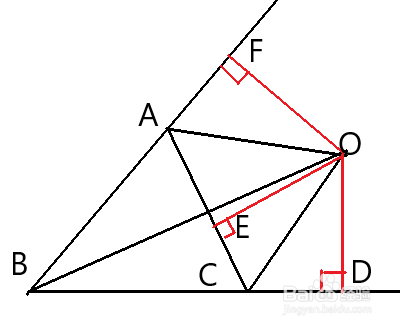
2、旁心到三角形三边的距离相等。如图，点O是△ABC的旁心，OD垂直BC于点D，OE垂直AC于点E，OF垂直BA于点F，则有结论：OD=OE=OF。

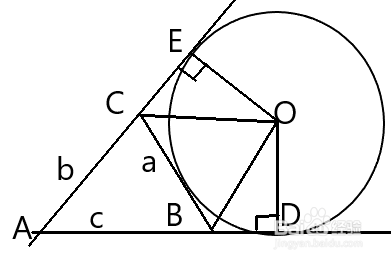
3、旁心张角：三角形两个外角平分线的夹角就是三角形旁心张角。如图，OC平分∠BCE，OB平分∠CBD，则有结论：∠BOC=90°-1/2∠CAB。

4、如图，a、b、c是△ABC的三边，点O是△ABC的旁心，OD垂直AB于点D，OE垂直AC于点E，则有结论：AD=AE=（a+b+c）/2。

5、如图，在△ABC中，OB平分∠ABC，OC平分∠ACD，

则有结论：∠BOC=1/2∠A。

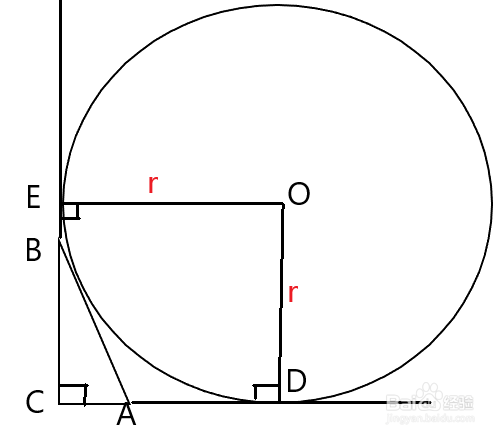
6、直角三角形斜边上的旁切圆半径等于三角形周长的一半。在Rt△ABC中，

∠ACB=90°，点O 是斜边AB边上的旁切圆的圆心，则有结论：

R=（a+b+c）/2。