如何在MATLAB中求导?
1、Y = diff(X) 计算沿大小不等于 1 的第一个数组维度的 X 相邻元素之间的差分:
如果 X 是长度为 m 的向量,则 Y = diff(X) 返回长度为 m-1 的向量。Y 的元素是 X 相邻元素之间的差分。
Y = [X(2)-X(1) X(3)-X(2) ... X(m)-X(m-1)]
如果 X 是不为空的非向量 p×m 矩阵,则 Y = diff(X) 返回大小为 (p-1)×m 的矩阵,其元素是 X 的行之间的差分。
Y = [X(2,:)-X(1,:); X(3,:)-X(2,:); ... X(p,:)-X(p-1,:)]
如果 X 是 0×0 的空矩阵,则 Y = diff(X) 返回 0×0 的空矩阵。
2、创建一个向量,然后计算元素之间的差分。
在MATLAB命令行输入:
X = [1 1 2 3 5 8 13 21];
Y = diff(X)

3、Y = diff(X,n) 通过递归应用 diff(X) 运算符 n 次来计算第 n 个差分。在实际操作中,这表示 diff(X,2) 与 diff(diff(X)) 相同。
4、创建一个 3×3 矩阵,然后计算各行之间的一阶差分。
在MATLAB命令行输入:
X = [1 1 1; 5 5 5; 25 25 25];
Y = diff(X)

5、Y = diff(X,n,dim) 是沿 dim 指定的维计算的第 n 个差分。dim 输入是一个正整数标量。
6、创建一个向量,然后计算元素之间的二阶差分。
在MATLAB命令行输入:
X = [0 5 15 30 50 75 105];
Y = diff(X,2)
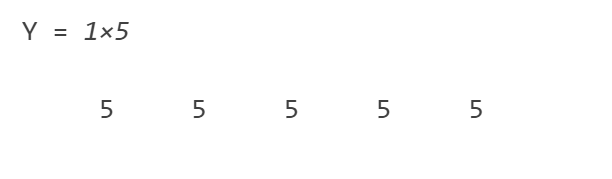
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:29
阅读量:155
阅读量:76
阅读量:72
阅读量:113