实数的加法群和正实数的乘法群同构？

1、实数的加法群，指的是全体实数的集合，在加法规则下构成的群，它满足成为一个群的所有要求。

2、全体整数构成整数加法群，是实数加法群的子群。

还可以有有理数加法群。

3、全体偶数也能构成一个群，可以称为偶数的加法群。这是整数加法群的子群，也是实数加法群的子群。

除此以外，还有：3的倍数的加法群、n的倍数的加法群。

4、奇数集合不能构成加法群，因为里面没有单位元，而且不能保持封闭性。

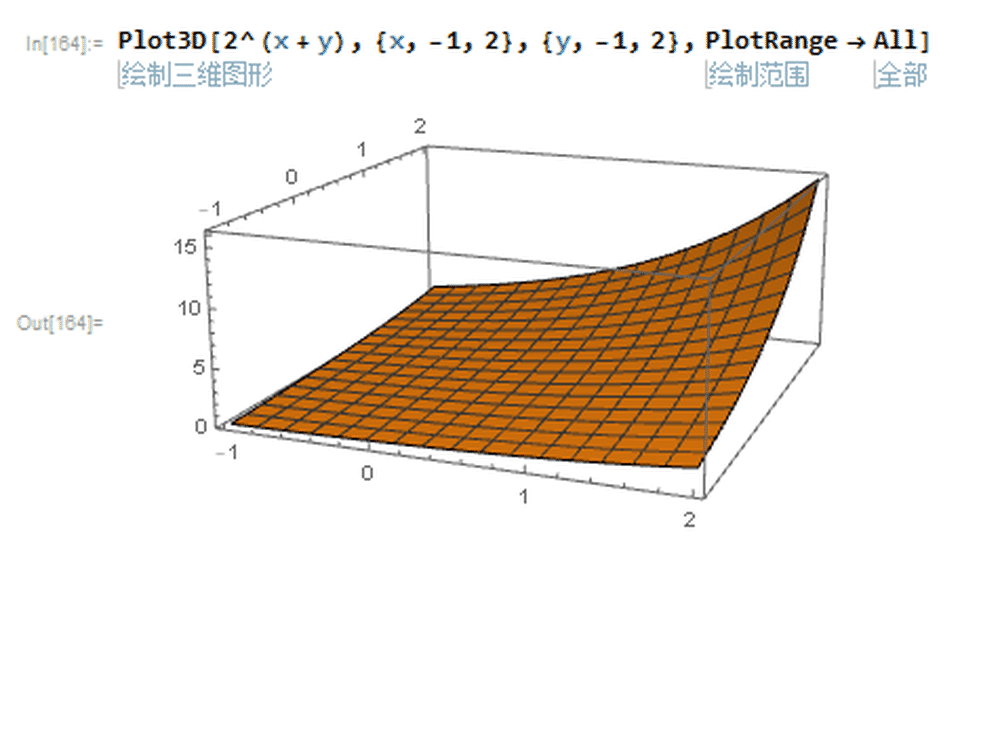
1、设x是一个实数，那么2^x就是一个正实数，而且是一一对应的。

2、在这个规则下，x+y就对应着2^(x+y)=(2^x）*(2^y)。

这说明，元素之间的相互作用也是一一对应的。

3、单位元也相互对应：

1=2^0，0=Log[1]。

综上所述，实数加法群和正实数乘法群确实是同构的。