【微分几何】怎么实现3D图形的旋转？

1、首先，用参数方程来绘制一个3D曲面：

aa=ParametricPlot3D[{2 Cos[u], Cos[v], Sin[u] Sin[v]*7/10},

  {u, 0, 2 Pi}, {v, 0, Pi}, PlotRange -> All, Axes -> False, Boxed -> False, 

  ImageSize -> {365, 365}, PlotPoints -> 100]

这个曲面看起来像是一个枕头。

2、查看曲面的时候，用Show来重新展示这个曲面：

Show[aa, ImageSize -> {365, 365}]

3、让曲面绕着z轴旋转一周：

Manipulate[

 Show[aa, ImageSize -> {365, 365},

   ViewPoint -> 2 {Cos[u], Sin[u], 0},

   SphericalRegion -> True], {u, 0, 2 Pi}]

这里采用交互模式，展示动画效果。

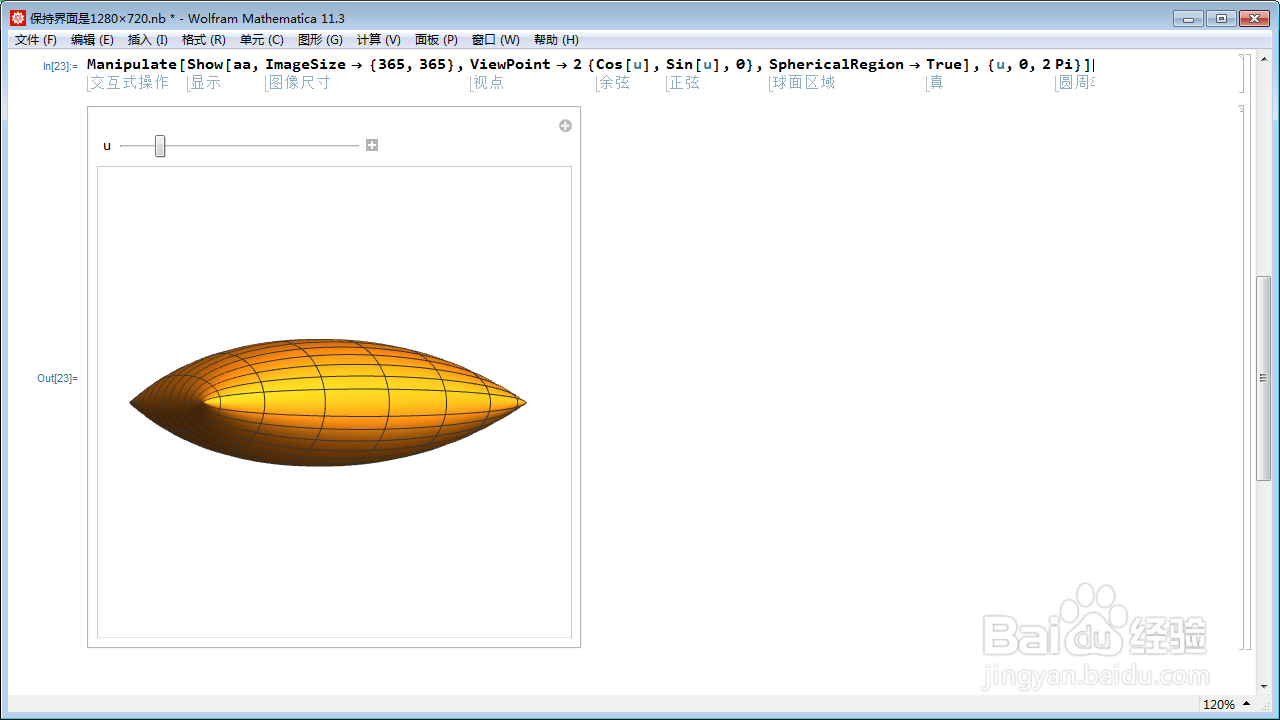
4、绕着y轴旋转一周，初步修改代码：

Manipulate[

 Show[aa, ImageSize -> {365, 365}, ViewPoint -> 2 {Cos[u], 0, Sin[u]},

   SphericalRegion -> True], {u, 0, 2 Pi}]

明显地，这个不是真正的旋转一周，中途，曲面发生了翻转。

5、加入额外的观察限制条件：

Manipulate[

 Show[aa, ImageSize -> {365, 365}, ViewPoint -> 2 {Cos[u], 0, Sin[u]},

   ViewVertical -> {0, 1, 0}, SphericalRegion -> True], {u, 0, 2 Pi}]

这时候曲面不会发生翻转。

6、ViewPoint指定的是观察点；

ViewVertical指定的是观察方向，这个方向始终是朝向正上方。

这两个观察限制条件，都可以用参数来表示：

Manipulate[

 Show[aa, ImageSize -> {365, 365}, ViewPoint -> 2 {Cos[u], 0, Sin[u]},

   ViewVertical -> {-Sin[u], 0, Cos[u]}, SphericalRegion -> True], {u,

   0, 2 Pi}]