计算过(2,4)圆x^2+y^2=1割线的中点轨迹方程
1、 介绍用参数轨迹法等由圆x^2+y^2=1外一点p(2,4)引圆的割线交圆于A、B两点,求弦AB的中点M的轨迹方程。
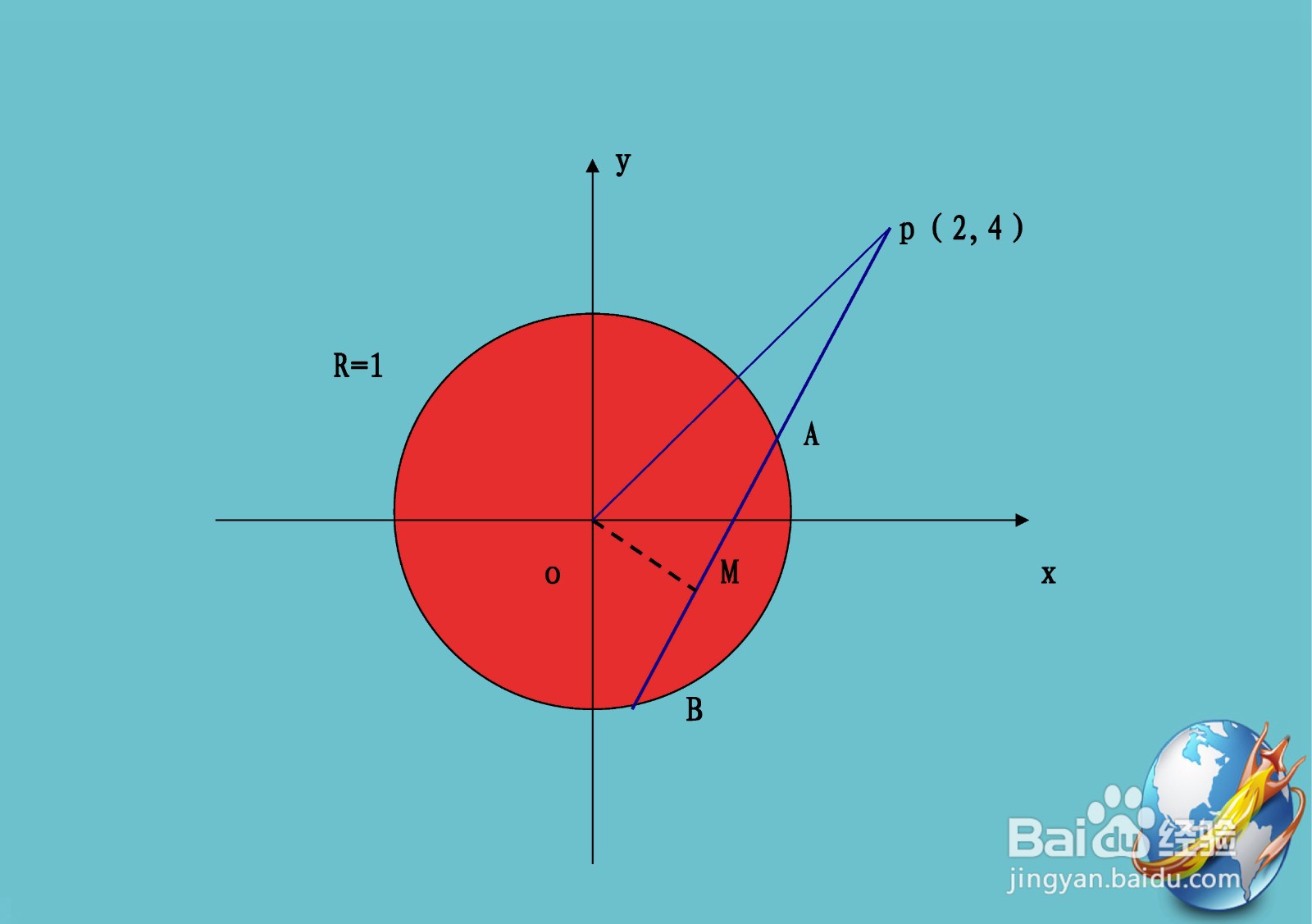
2、 此时圆x^2+y^2=1与点p(2,4)在同一坐标系示意图为。
1、设弦AB的中点M的坐标为M(x,y),连接OP,0M,
则OM⊥AB,在△OMP中,由两点间的距离公式和勾股定理有OP2=PM2+OM2,即:
(2-0)2+(4-0)2=[(x-2)2+(y-4)2]+[(x-0)2+(y-0)2]
22+42=x2-4x+22+y2-8y+42+x2+y2,
0=x2-4x+y2-8y+x2+y2,故:
x2+y2-2x-4y=0,其中:-1≤x≤1.
为所求圆割线中点的轨迹方程。

2、根据题设条件,判断并确定轨迹的曲线类型,运用待定系数法求出曲线方程。

3、解:∵M(x,y)是AB的中点,所以OM⊥AB,点M的轨迹是以OP为直径的圆,圆心为(1,2),半径r=|op|,圆的方程为:
(x-1)2+(y-2)2=[(2-0)2+(4-0)2],化简,得:
x2-2x+1+y2-4y+4=*22+*42,即所求圆割线中点的轨迹方程为:x2+y2-2x-4y=0,其中:-1≤x≤1.

4、将问题转化为求两直线的交点轨迹问题。因为动点M可看作直线OM与割线PM的交点,而由于它们的垂直关系,从而获得解法。
解:设过p点的割线的斜率为k,则过p点的割线方程为:y-4=k(x-2),
∵OM⊥AB且过原点,
∴OM的方程为y=-*x,即:ky=-x。
这两条直线的交点就是M点的轨迹。

5、由割线方程得:k=(y-4)/(x-2) ,代入OM方程得:
(y-4)/(x-2)*y=-x,化简得:
y(y-4)=-x(x-2)
y2-4y=-x2+2x,即所求轨迹方程为:
x2+y2-2x-4y=0,其中:-1≤x≤1.

6、将动点坐标表示成某一中间变量即参数的函数,再设法消去参数。由于动点M(xi,yi)随直线的斜率变化而发生变化,所以动点M的坐标是直线斜率的函数。

7、解:设过P点的割线方程为:y-4=k(x-2), 它与圆
x2+y2=R2的两个交点为A、B,AB的中点为M.解方程组:
y-4=k(x-2),
x2+y2=1
消去y得:x2+(kx-2k+4)2=1,即:
(1+k2)x2-2k(2k-4)x+(4-2k)2-1=0,


8、解:设M(x,y),A(x1,y1),B(x2,y2),则:
x1+x2=2x,y1+y2=2y,
∵x12+y12=1,x22+y22=1,两式减得:
(x2-x1)(x2+x1)+(y2-y1)(y1+y2)=0,即:
化简得:
y(4-y)+x(2-x)=0,即所求轨迹方程为:
x2+y2-2x-4y=0,其中:-1≤x≤1.

