原创方法证明1+2+3+......+n前n项求和公式

1、我们先自定义：一个单位对应一个点

正如“1”对应一个苹果；“2”对应两个苹果；“3”对应三个苹果

如下

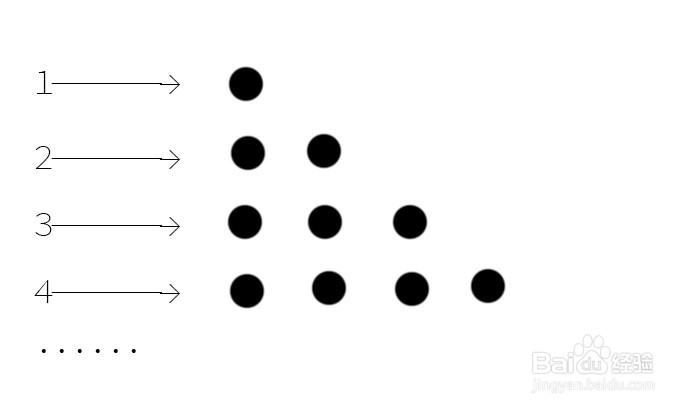
2、将 点阵 排成 三角阵

所以 数列1+2+3+......+n 的和即为 三角阵的点数，如下

3、将三角阵复制，拼接至右方，形成个 矩形点阵

（其实也没这必要，但为了好理解这方法......）

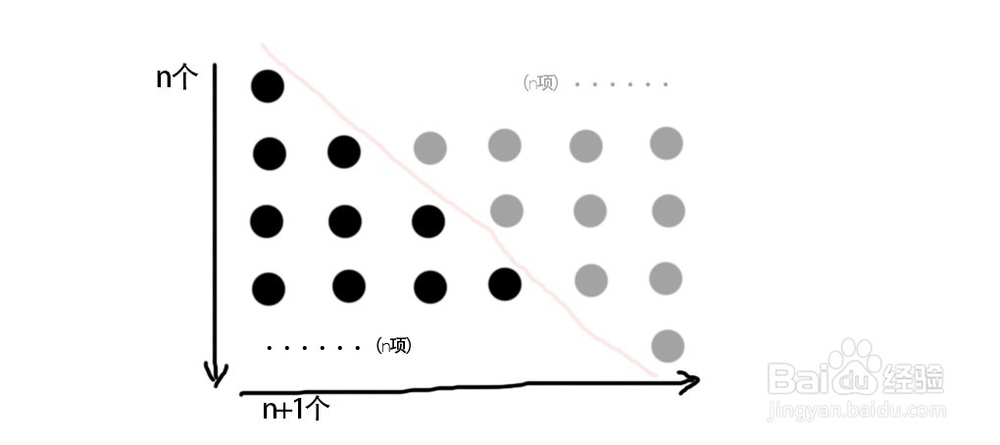
4、然后，到这大家都想到了吧，就像算面积一样

算出 矩形点阵 内含的点数>>>除以2>>>即为原三角阵点数 

故1+2+3+......+n = n(n+1)/2  ,即所求数列前n项和公式

（其实一开始直接算 三角点阵 就行了）

1、其实这有点类似于 定积分，理解以后，在学 定积分 就容易了

（定积分为高中数学内容）

————

至于1²+2²+3²+......+n²的推导，有点麻烦，不如高中的数学归纳法，在此不展开