y=(x^3+5x^2).(x-1)^2的图像示意图

1、函数的定义域∵x-1≠0，∴x≠1，即函数的定义域为：(-∞,1)∪(1,+∞）。

2、∵y=(x^3+5x^2)/(x-1)^2

∴dy/dx

=[(3x^2+10x)(x-1)^2-2(x-1)(x^3+5x^2)]/(x-1)^4

=[(3x^2+10x)(x-1)-2(x^3+5x^2)]/(x-1)^3

=x[(3x+10)(x-1)-2(x^2+5x)]/(x-1)^3

=x(x^2-3x-10)/(x-1)^3

3、   如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加;反之，若x∈D时，f'(x)<0,则称函数y=f(x)在区间D内单调减少。

4、∵dy/dx=(x^3-3x^2-10x)/(x-1)^3

∴d^2y/dx^2

=[(3x^2-6x-10)(x-1)^3-3(x^3-3x^2-10x)(x-1)^2]/(x-1)^6

=[(3x^2-6x-10)(x-1)-3(x^3-3x^2-10x)]/(x-1)^4

=(26x+10)/(x-1)^4

=2(13x+5)/(x-1)^4  

5、令d^2y/dx^2=0,则：

则: 13x+5=0，即x=-5/13.

(1).当x∈(-∞，-5/13)时，d^2y/dx^2＜0，

此时函数y为凸函数；

(2).当x∈(-5/13,1)∪(1，+∞)时，

d^2y/dx^2＞0，此时函数y为凹函数。

6、判断函数在正负无穷大处和不定义点处的极限。

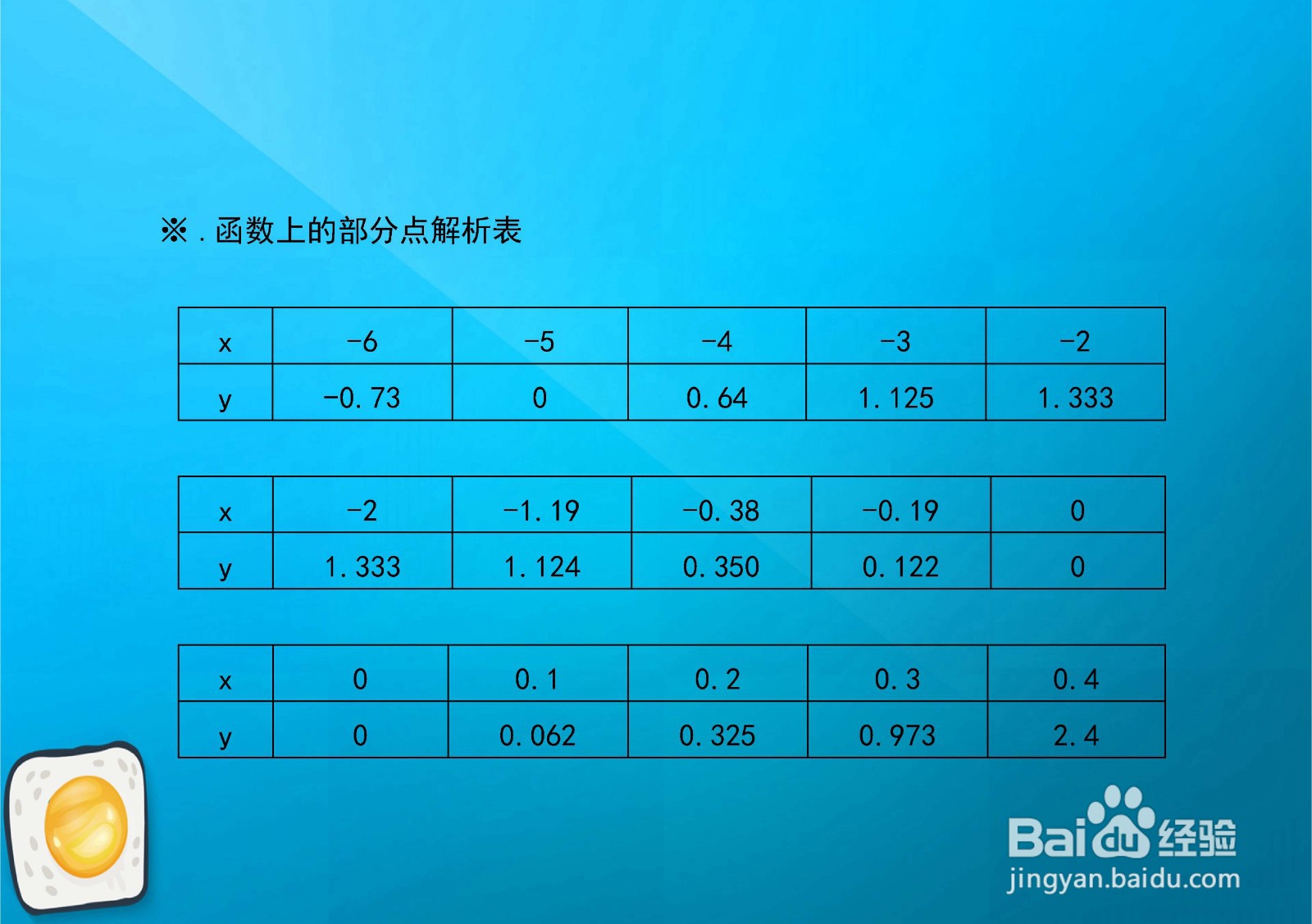
7、x -2 -1.19 -0.38 -0.19 0

y 1.333 1.124 0.350 0.122 0

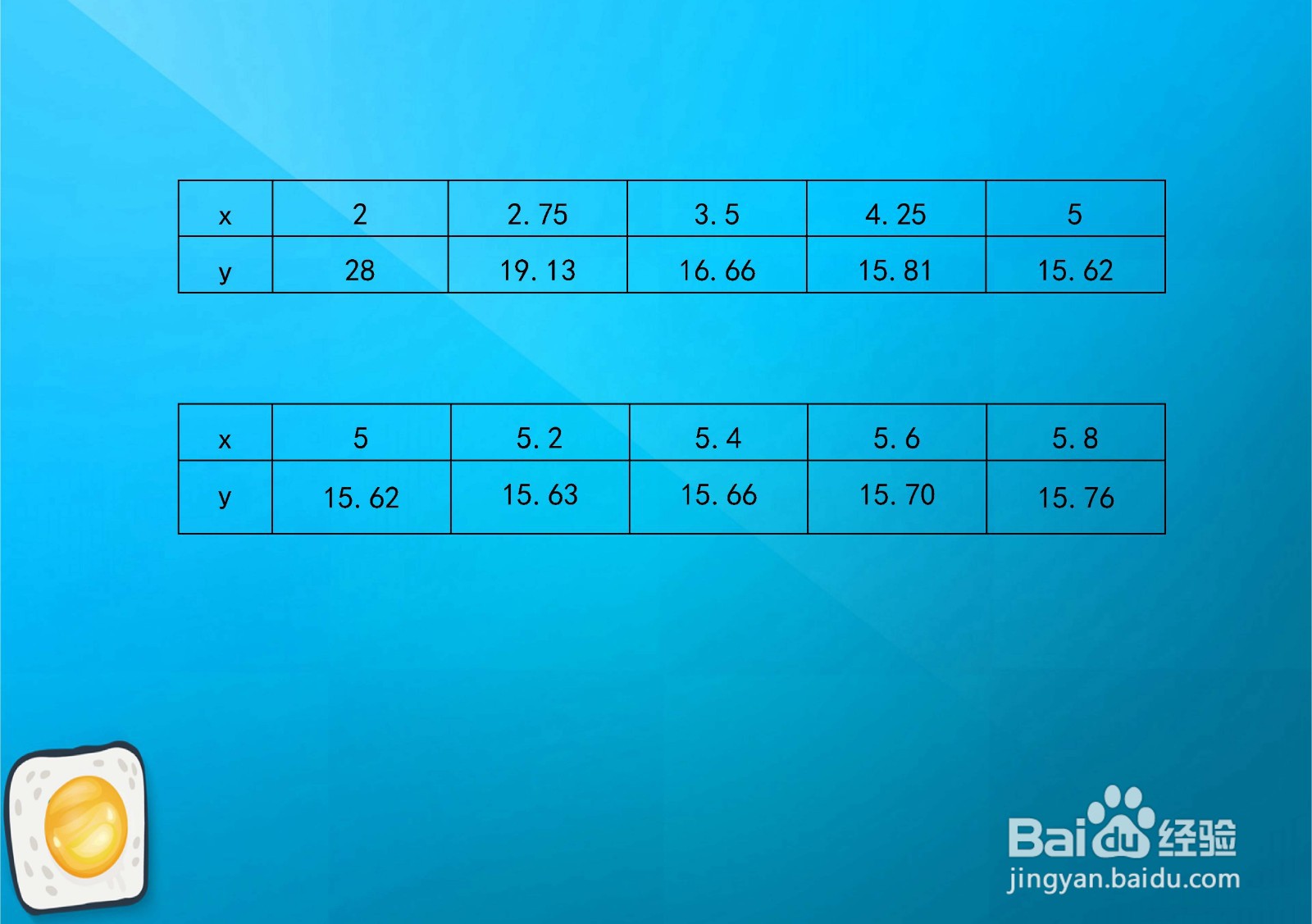
8、综合以上函数的定义域、值域、单调性、凸凹性和极限等性质，函数的示意图如下：