如何证明直角三角形斜边上的中线等于斜边的一半

1、给定直角三角形ABC，∠A是直角，斜边CD中点为D，连接线段AD。

2、取AB中点E，那么DE//AC。

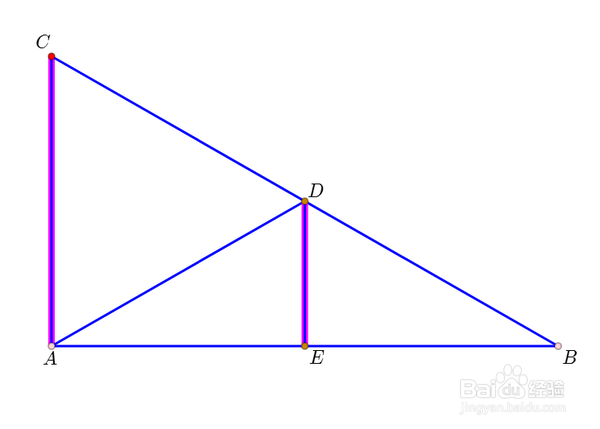
3、注意到，∠BAC是直角，所以∠DEB也是直角，即DE⊥AB。

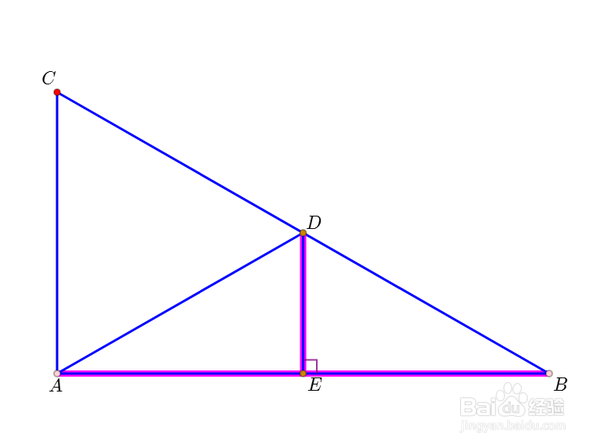
4、又因为E是线段AB中点，所以DE是AB的中垂线，所以，AD=BD。这已经说明了，AD=BC/2。

5、反之，命题也成立。即，如果AD=BD=CD，那么∠BAC是直角。下面开始证明：因为AD=BD，所以∠DAB=∠DBA。

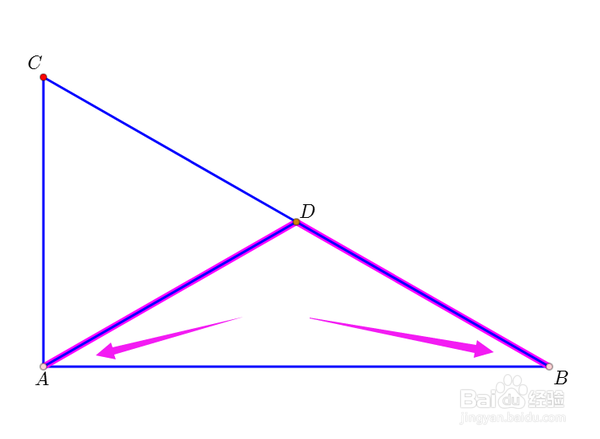
6、同样的，有∠DAC=∠DC钽吟篑瑜A。又因为△ABC内角和是180°，所以：∠DAB+∠DAC+∠DBA+∠DCA=180°；2(∠DAB+鹳帕鄯区∠DAC)=180°；所以∠DAB+∠DAC=90°，∠BAC是直角。

7、如果A关于D的对称点是E，那么四边形ABED是矩形。这是步骤6的结论的直接推论。