四川省考公务员考试行测数量关系题怎么运算求解

1、运用说明

从选项入手，代入某个选项后，如果不符合已知条件，或推出矛盾，则可排除此选项。

1）直接代入：把选项一个一个代入验证，直至得到符合题意的选项为激耕止。

2）选择耕胆追性代入：根据数的特性(奇偶性、整除特性、尾数特性、余数特性等)先筛选，再代入排除的方法。

2、适用题型

运用于多位数问题、不定方程问题、剩余问题、年龄问题、复杂行程问题、和差倍比问题等。

具体撤温示例及运用如图1

1、运用说明

在题目所给的范围内取一个恰当的特殊值直接代入，简化问题。特殊值法须选取满足题干的特殊数、特殊点、特殊函数、特殊数列或特殊图形代替一般的情况，并由此计算出结果，从而快速解题。

2、适用题型

和差倍比问题、行程问题、工程问题、浓度问题、利润问题、几何问题等。

如，工程问题、浓度问题相关的比例问题，一般将特殊值设为1；涉及多个比例的问题时，若将数值整数化，可设特殊值为总量的最小公倍数。

具体示例及运用如图2

1、运用说明

图解法运用的图形包括线段图、网状图/树状图、文氏图和表格等。

1）线段图：用线段来表示数字和数量关系的方法。一般，用线段来表示量与量之间的倍数关系或者整个运动过程等，来解决和差倍比问题、行程问题等。

2）网状图或树状图

①网状图

一般由三组斜线组成，各组分别代表一种事物。从各自的顶端向下面走，分布率就从100%向下降。即用一个三角形网状表示某个对象在三个方面的分布情况。

②树状图

通过列树状图列出某事件的所有可能的结果，求出其概率。

3）文氏图

用一条封闭曲线直观地表示集合及其关系的图形，能直观地表现出集合之间的关系。其中圆表示一个类，两个圆相交，其相交部分就是两个类的共同部分。两个圆不相交，则说明这两个类没有共同元素。

4）表格

将多次操作问题和还原问题中的复杂过程一一呈现，也可以用表格理清数量关系，帮助列方程。

2、适用题型

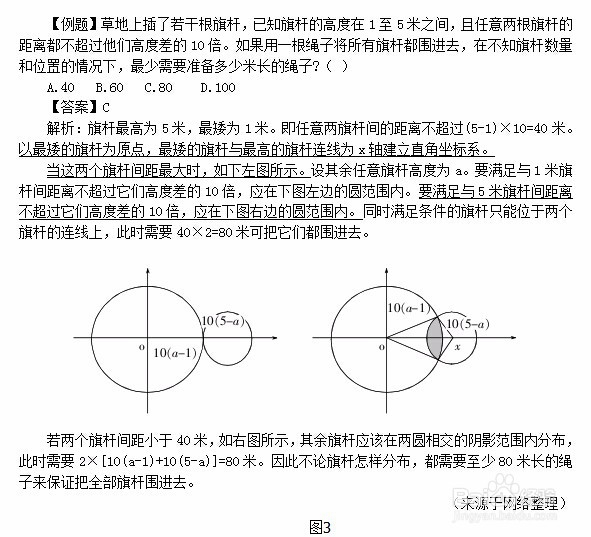
几何问题、行程问题、年龄问题、容斥问题等强调分析过程的题型中运用。

如，网状图或树状图可用于排列组合、推理问题或时间安排类的对策分析问题。

具体示例及运用如图3

1、运用说明

利用分与合两种不同的思维解答数学运算的方法。

1）分类讨论

指当不能对问题所给的对象进行统一研究时，需要对研究对象按某个标准进行分类，逐类研究，最后将结论汇总得解的方法。

需注意分类标准统一，分类情况不遗漏、不重复，不越级讨论。一般是多种情况分类讨论后，再利用加法原理求出总的情况数。

2）整体法

①将某一部分看成一个整体，在问题中总是一起考虑，而不单独求解；

②不关心局部关系，只关心问题的整体情况，直接根据整体情况来考虑关系，这种形式经常用于平均数问题。

具体示例及运用如图4

2、适用题型

一般适用于排列组合与概率问题、解方程等。

1、运用说明

1）分析极端状态

先分析并找出问题的极限状态，再与题干条件相比较，作出相应调整，得出所求问题的解。

2）考虑极限图形与极限位置

①极限图形：主要是利用一些几何知识。

如，对于空间几何体，当表面积相同时，越趋近于球体的体积越大；同理，当体积相同时，越趋近于球体的表面积越小。

②极限位置：先找到图形中满足条件的极端位置，再判断极端位置与题中所求之间的关系，进而求出题目答案。

2、适用题型

一般适用于鸡兔同笼问题、对策分析类问题等。

具体示例及运用如图5

1、运用说明

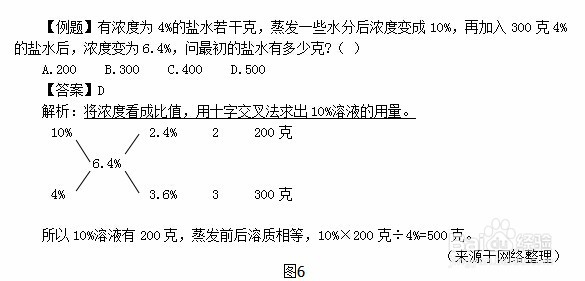
1）十字交叉法是由盈亏思想得到的，即多的总量等于少的总量。

2）用“交叉十字”来求两个部分混合后平均量，包含“部分平均量、混合平均量、交叉作差项、部分平均量分母的最简比”。

设第一部分的平均值为a，第二部分的平均值为b(这里假设a>b) ，混合后的平均值为r。得到等式：(r-b)/(a-r)=A/B.

3）运用步骤

①找出各个部分平均值和总体平均值；

②平均值间交叉作差，写出部分对应量或对应量的比；

③利用比例关系解答。

2、适用题型

一般用于两个部分相关的平均值问题，且运用的前提是已知总体平均值。

如，多个“比值”的混合问题，“比值”可以是平均数、浓度、利润率、增长率、折扣、比重等。

具体示例及运用如图6